JEE Advance - Physics (2009 - Paper 1 Offline - No. 9)
For the circuit shown in the figure
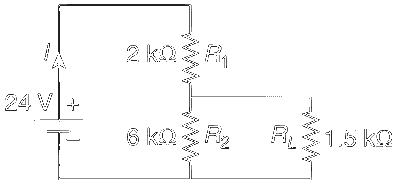
Explanation
The current in the net circuit is
$$I = {V \over {{R_{effective}}}}$$
$$ = {V \over {{R_1} + [({R_2}{R_L})/({R_1} + {R_L})]}}$$
$$ = {{24} \over {2 \times {{10}^{ - 3}} + [(6 \times 1.5 \times {{10}^{ - 6}})/(7.5 \times {{10}^{ - 3}})]}} = 7.5$$ mA

The potential across $$R_L$$ is
$${V_L} = I \times {{{R_2}{R_L}} \over {{R_2} + {R_L}}}$$
$$ = 7.5 \times {10^{ - 3}} \times 1.2 \times {10^3} = 9$$ V
Therefore,
$$I = {9 \over {{R_L}}} = 6$$ mA
The ratio of power dissipated in $$R_1$$ and $$R_2$$ is
$${{I{R_1}} \over {(I - i){R_2}}} = {{{{(7.5 \times {{10}^{ - 3}})}^2} \times 2 \times {{10}^3}} \over {{{(1.5 \times {{10}^{ - 3}})}^2}6 \times {{10}^3}}} = 0.75$$ J
The power dissipated in $$R_L$$ is
$${{V_L^2} \over {{R_L}}} = {{{9^2}} \over {1.5 \times {{10}^3}}} = 54$$ mJ
If $$R_1$$ and $$R_2$$ are interchanged, then
$$I' = {V \over {{R_{effective}}}}$$
$$ = {V \over {{R_2} + [({R_1}{R_L})/({R_L} + {R_1})]}}$$
$$ = {{24} \over {6 \times {{10}^{ - 3}} + [(2 \times 1.5 \times {{10}^{ - 6}})/3.5 \times {{10}^{ - 3}}]}} = 3.5$$ mA
Hence, the voltage drop across the load is
$$V{'_L} = I \times {{{R_1}{R_L}} \over {{R_1} + {R_L}}} = 1$$ V
Therefore, $$i' = 2$$ mA. The magnitude of the power dissipated is the ratio between $${i^2}$$ and $${(i')^2}$$:
$${{{P_1}} \over {{P_2}}} = {{{i^2}} \over {{{(i')}^2}}} = {{{6^2}} \over {{2^2}}} = 9$$
Comments (0)


