JEE Advance - Physics (2009 - Paper 1 Offline - No. 7)
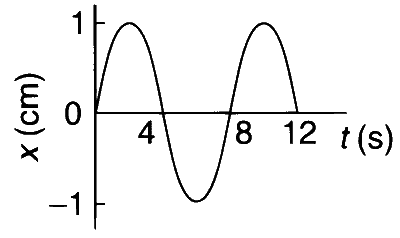
The $$x$$-$$t$$ graph of a particle undergoing simple harmonic motion is shown in the figure. The acceleration of the particle at $$t=4/3$$ s is
$${{\sqrt 3 } \over {32}}{\pi ^2}$$ cm/s$$^2$$
$${{ - {\pi ^2}} \over {32}}$$ cm/s$$^2$$
$${{ {\pi ^2}} \over {32}}$$ cm/s$$^2$$
$$ - {{\sqrt 3 } \over {32}}{\pi ^2}$$ cm/s$$^2$$
Explanation
The equation of single harmonic motion is $$x = A\sin \left( {{{2\pi } \over T}t} \right)$$, where A is amplitude and T is the time period of the motion.
From the given figure, $$A = 1$$ and $$T = 8$$. Thus,
$$x = \sin \left( {{\pi \over 4}t} \right)$$
The acceleration is
$$a = {{{d^2}x} \over {d{t^2}}} = {{ - {\pi ^2}} \over {16}}\sin \left( {{\pi \over 4}t} \right)$$
At time $$t = {4 \over 3}s$$, the acceleration is
$$a = {{ - {\pi ^2}} \over {16}}\sin \left( {{\pi \over 4} \times {4 \over 3}} \right) = - {{\sqrt 3 } \over {32}}{\pi ^2}$$ cm/s$$^2$$
Comments (0)


