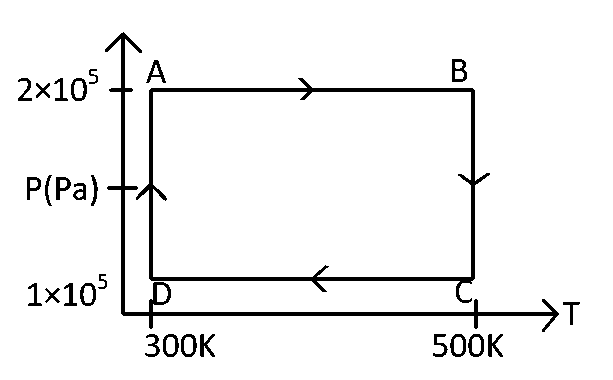
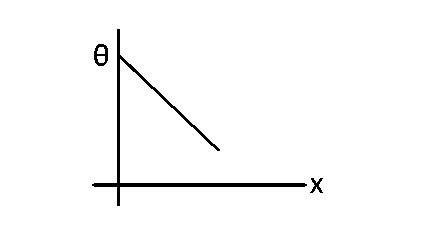JEE MAIN - Physics (2009)
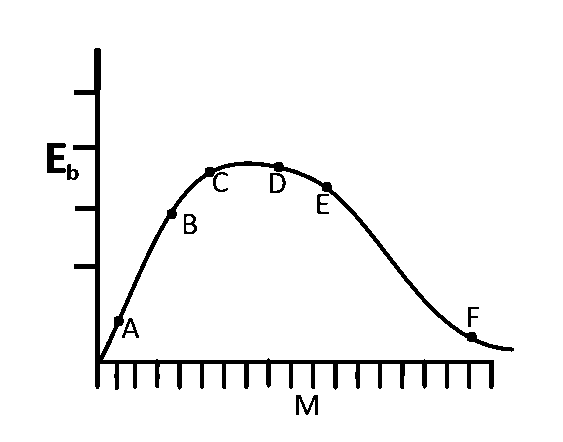
The above is a plot of binding energy per nucleon $${E_b},$$ against the nuclear mass $$M;A,B,C,D,E,F$$ correspond to different nuclei. Consider four reactions :
$$\eqalign{
& \left( i \right)\,\,\,\,\,\,\,\,\,\,A + B \to C + \varepsilon \,\,\,\,\,\,\,\,\,\,\left( {ii} \right)\,\,\,\,\,\,\,\,\,\,C \to A + B + \varepsilon \,\,\,\,\,\,\,\,\,\, \cr
& \left( {iii} \right)\,\,\,\,\,\,D + E \to F + \varepsilon \,\,\,\,\,\,\,\,\,\,\left( {iv} \right)\,\,\,\,\,\,\,\,\,F \to D + E + \varepsilon ,\,\,\,\,\,\,\,\,\,\, \cr} $$
where $$\varepsilon $$ is the energy released? In which reactions is $$\varepsilon $$ positive?
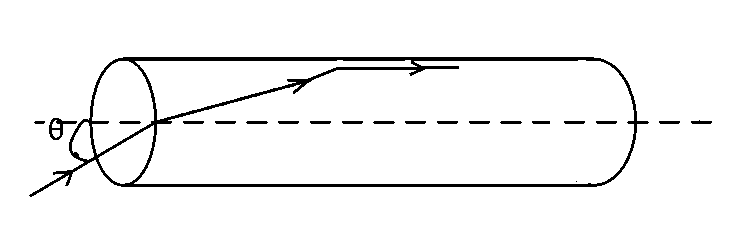
The incident angle $$\theta $$ for which the light ray grazes along the wall of the rod is :
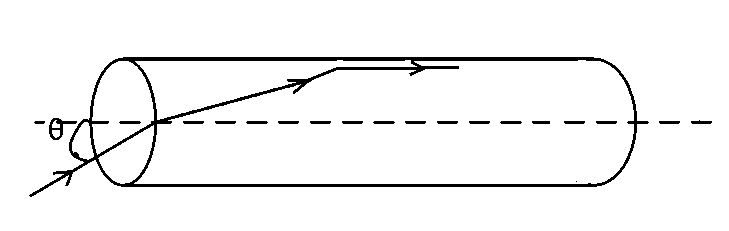
The incident angle $$\theta $$ for which the light ray grazes along the wall of the rod is :
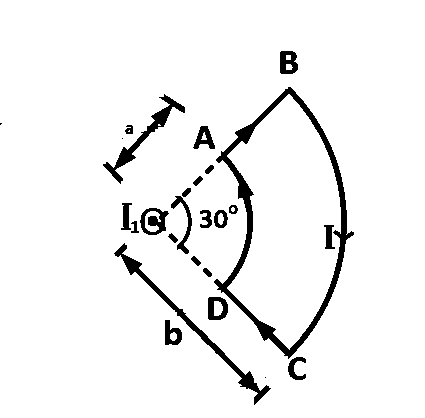
Due to the presence of the current $${I_1}$$ at the origin:
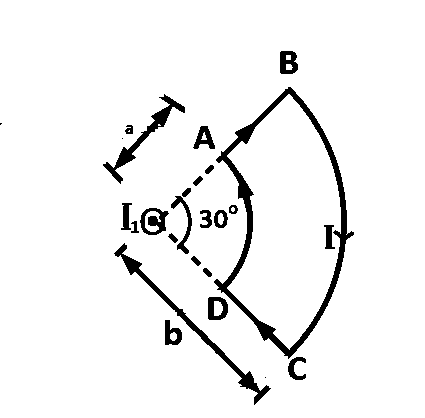
The magnitude of the magnetic field $$(B)$$ due to the loop $$ABCD$$ at the origin $$(O)$$ is :
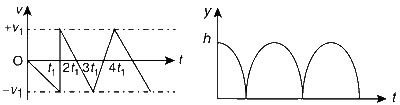
Then the velocity as a function of time and the height as a function of time will be :
Statement-2 : The net work done by a conservative force on an object moving along a closed loop is zero.
Statement - 2: $$R = {R_0}\left( {1 + \alpha \,\Delta t} \right)$$ is valid only when the change in the temperature $$\Delta T$$ is small and $$\Delta T = \left( {R - {R_0}} \right) < < {R_0}.$$