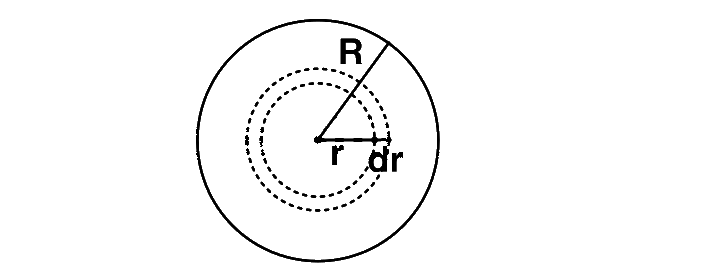
Let us consider a spherical shell of thickness $$dx$$ and radius $$x.$$ The volume of this spherical shell $$ = 4\pi {r^2}dr.$$

The charge enclosed within shell

$$ = {{{Q_r}} \over {\pi {R^4}}}\left[ {4\pi {r^2}dr} \right]$$

The charge enclosed in a sphere of radius $${r_1}$$ is

$${{4Q} \over {{R^4}}}\int\limits_0^{{r_1}} {{r^3}} dr$$

$$ = {{4Q} \over {{R^4}}}\left[ {{{{r^4}} \over 4}} \right]_0^{{r_1}}$$

$$ = {Q \over {{R^4}}}r_1^4$$

$$\therefore$$ The electric field at point $$p$$ inside the sphere at a distance $${r_1}$$ from the center of the sphere is

$$E = {1 \over {4\pi { \in _0}}}{{\left[ {{Q \over {{R^4}}}r_1^4} \right]} \over {r_1^2}}$$

$$ = {1 \over {4\pi { \in _0}}}{Q \over {{R^4}}}r_1^2$$