JEE MAIN - Physics (2009 - No. 8)
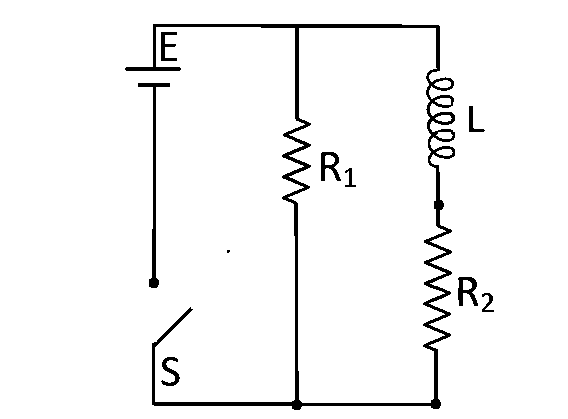
An inductor of inductance $$L=400$$ $$mH$$ and resistors of resistance $${R_1} = 2\Omega $$ and $${R_2} = 2\Omega $$ are connected to a battery of $$emf$$ $$12$$ $$V$$ as shown in the figure. The internal resistance of the battery is negligible. The switch $$S$$ is closed at $$t=0.$$ The potential drop across $$L$$ as a function of time is :

$${{12} \over t}{e^{ - 3t}}V$$
$$6\left( {1 - {e^{ - t/0.2}}} \right)V$$
$$12{e^{ - 5t}}V$$
$$6{e^{ - 5t}}V$$
Explanation
Growth in current in $$L{R_2}$$ branch when switch is closed is given by
$$i = {E \over {{R_2}}}\left[ {1 - {e^{ - {R_2}t/L}}} \right]$$
$$ \Rightarrow {{di} \over {dt}} = {E \over {{R_2}}}.{{{R_2}} \over L}.{e^{ - {R_{2t/L}}}}$$
$$ = {E \over L}{e^{{{{R_2}t} \over L}}}$$
Hence, potential drop across
$$L = \left( {{E \over L}{e^{ - {R_2}t/L}}} \right)L = E{e^{ - {R_2}t/L}}$$
$$ = 12{e^{ - {{2t} \over {400 \times {{10}^{ - 3}}}}}} = 12{e^{ - 5t}}V$$
$$i = {E \over {{R_2}}}\left[ {1 - {e^{ - {R_2}t/L}}} \right]$$
$$ \Rightarrow {{di} \over {dt}} = {E \over {{R_2}}}.{{{R_2}} \over L}.{e^{ - {R_{2t/L}}}}$$
$$ = {E \over L}{e^{{{{R_2}t} \over L}}}$$
Hence, potential drop across
$$L = \left( {{E \over L}{e^{ - {R_2}t/L}}} \right)L = E{e^{ - {R_2}t/L}}$$
$$ = 12{e^{ - {{2t} \over {400 \times {{10}^{ - 3}}}}}} = 12{e^{ - 5t}}V$$
Comments (0)


