JEE MAIN - Physics (2009 - No. 13)
Consider a rubber ball freely falling from a height $$h=4.9$$ $$m$$ onto a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic.
Then the velocity as a function of time and the height as a function of time will be :
Then the velocity as a function of time and the height as a function of time will be :
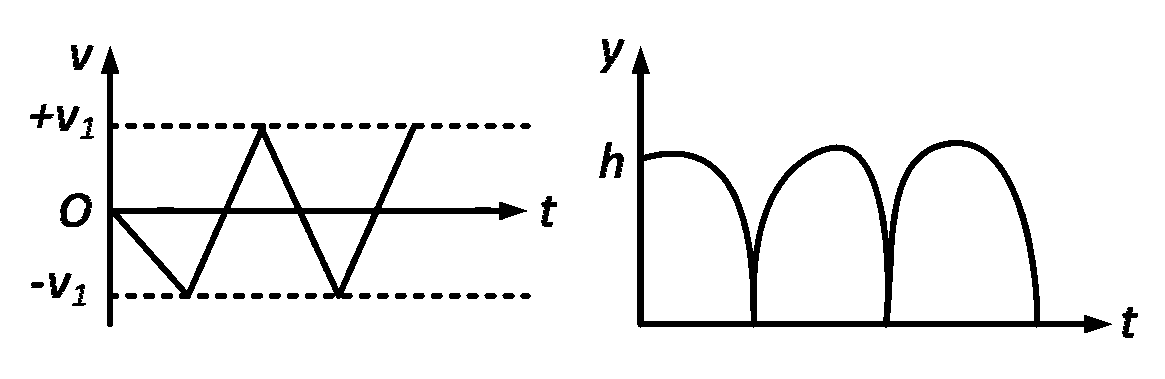
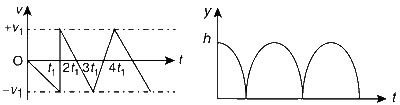
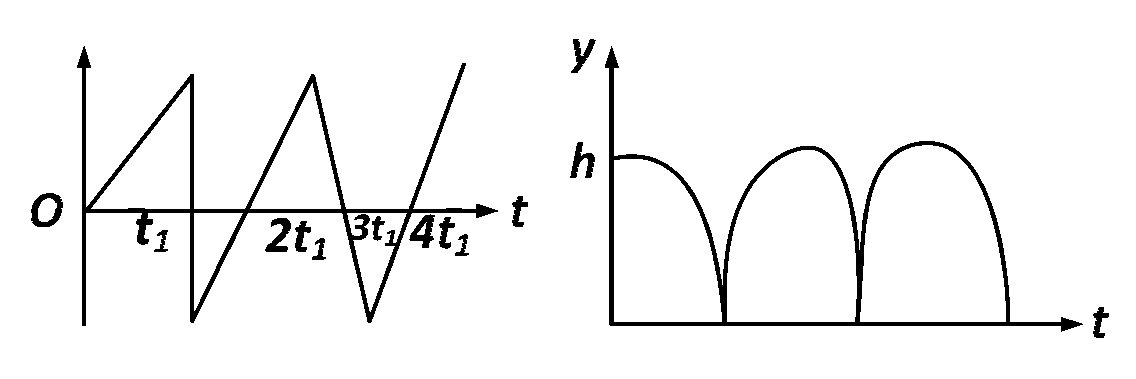
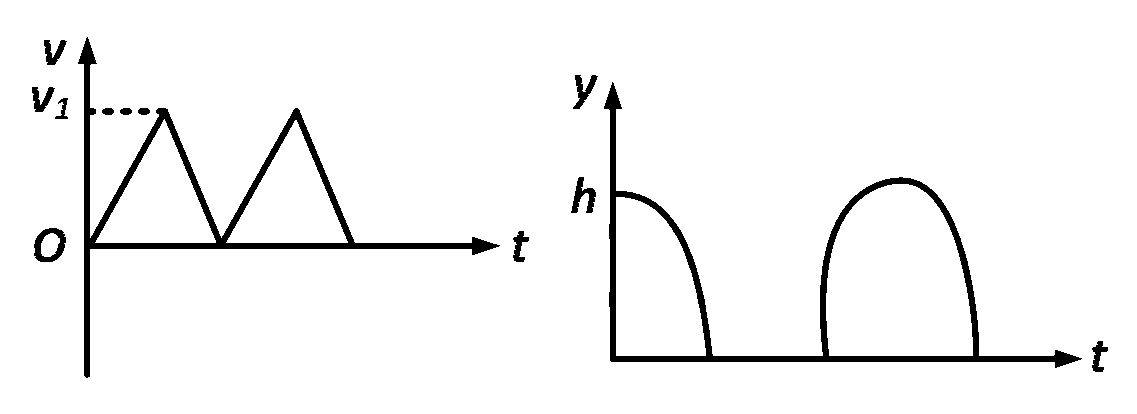
Explanation
For downward motion :
$$v=-gt$$
The velocity of the rubber ball increases in downward direction and we get a straight line between $$v$$ and $$t$$ with a negative slope.
Also applying $$y - {y_0} = ut + {1 \over 2}a{t^2}$$
We get $$y - h = - {1 \over 2}g{t^2} \Rightarrow y = h - {1 \over 2}g{t^2}$$
The graph between $$y$$ and $$t$$ is a parabola with $$y=h$$ at $$t=0.$$ As time increases $$y$$ decreases.
For upward motion :
The ball suffer elastic collision with the horizontal elastic plate therefore the direction of velocity is reversed and the magnitude remains the same. Here $$v=u-gt$$ where $$u$$ is the velocity just after collision. As $$t$$ increases, $$v$$ decreases. We get a straight line between $$v$$ and $$t$$ with negative slope.
Also $$y = ut - {1 \over 2}g{t^2}$$
All these characteristics are represented by graph $$(B).$$
$$v=-gt$$
The velocity of the rubber ball increases in downward direction and we get a straight line between $$v$$ and $$t$$ with a negative slope.
Also applying $$y - {y_0} = ut + {1 \over 2}a{t^2}$$
We get $$y - h = - {1 \over 2}g{t^2} \Rightarrow y = h - {1 \over 2}g{t^2}$$
The graph between $$y$$ and $$t$$ is a parabola with $$y=h$$ at $$t=0.$$ As time increases $$y$$ decreases.
For upward motion :
The ball suffer elastic collision with the horizontal elastic plate therefore the direction of velocity is reversed and the magnitude remains the same. Here $$v=u-gt$$ where $$u$$ is the velocity just after collision. As $$t$$ increases, $$v$$ decreases. We get a straight line between $$v$$ and $$t$$ with negative slope.
Also $$y = ut - {1 \over 2}g{t^2}$$
All these characteristics are represented by graph $$(B).$$
Comments (0)


