JEE MAIN - Physics (2009 - No. 11)
A current loop $$ABCD$$ is held fixed on the plane of the paper as shown in the figure. The arcs $$BC$$ (radius $$= b$$) and $$DA$$ (radius $$=a$$) of the loop are joined by two straight wires $$AB$$ and $$CD$$. A steady current $$I$$ is flowing in the loop. Angle made by $$AB$$ and $$CD$$ at the origin $$O$$ is $${30^ \circ }.$$ Another straight thin wire steady current $${I_1}$$ flowing out of the plane of the paper is kept at the origin.
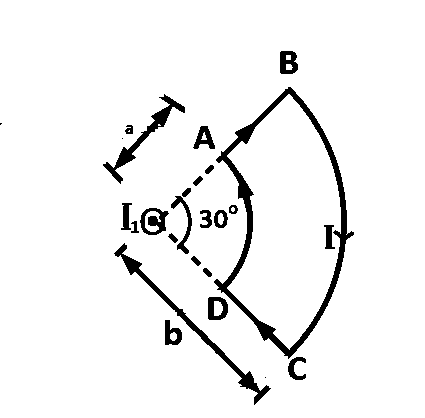

The magnitude of the magnetic field $$(B)$$ due to the loop $$ABCD$$ at the origin $$(O)$$ is :
$${{{\mu _0}I\left( {b - a} \right)} \over {24ab}}$$
$${{{\mu _0}I} \over {4\pi }}\left[ {{{b - a} \over {ab}}} \right]$$
$${{{\mu _0}I} \over {4\pi }}\left[ {2\left( {b - a} \right) + {\raise0.5ex\hbox{$\scriptstyle \pi $}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 3$}}\left( {a + b} \right)} \right]$$
zero
Explanation
The magnetic field at $$O$$ due to current in $$DA$$ is
$${B_1} = {{{\mu _0}} \over {4\pi }}{I \over a} \times {\pi \over 6}\,\,\,$$ (directed vertically upwards)
The magnetic field at $$O$$ due to current in $$BC$$ is
$${B_2} = {{{\mu _0}} \over {4\pi }}{I \over b} \times {\pi \over 6}$$ (directed vertically downwards)
The magnetic field due to current $$AB$$ and $$CD$$ at $$O$$ is zero.
therefore the net magnetic field is
$$B = {B_1} - {B_2}$$ (directed vertically upwards)
$$ = {{{\mu _0}} \over {4\pi }}{I \over a}{\pi \over 6} - {{{\mu _0}} \over {4\pi }}{I \over b} \times {\pi \over 6}$$
$$ = {{{\mu _0}I} \over {24}}\left( {{1 \over a} - {1 \over b}} \right)$$
$$ = {{{\mu _0}I} \over {24ab}}\left( {b - a} \right)$$
$${B_1} = {{{\mu _0}} \over {4\pi }}{I \over a} \times {\pi \over 6}\,\,\,$$ (directed vertically upwards)
The magnetic field at $$O$$ due to current in $$BC$$ is
$${B_2} = {{{\mu _0}} \over {4\pi }}{I \over b} \times {\pi \over 6}$$ (directed vertically downwards)
The magnetic field due to current $$AB$$ and $$CD$$ at $$O$$ is zero.
therefore the net magnetic field is
$$B = {B_1} - {B_2}$$ (directed vertically upwards)
$$ = {{{\mu _0}} \over {4\pi }}{I \over a}{\pi \over 6} - {{{\mu _0}} \over {4\pi }}{I \over b} \times {\pi \over 6}$$
$$ = {{{\mu _0}I} \over {24}}\left( {{1 \over a} - {1 \over b}} \right)$$
$$ = {{{\mu _0}I} \over {24ab}}\left( {b - a} \right)$$
Comments (0)


