JEE MAIN - Physics (2009 - No. 25)
Two wires are made of the same material and have the same volume. However wire $$1$$ has cross-sectional area $$A$$ and wire $$2$$ has cross-sectional area $$3A.$$ If the length of wire $$1$$ increases by $$\Delta x$$ on applying force $$F,$$ how much force is needed to stretch wire $$2$$ by the same amount?
$$4F$$
$$6F$$
$$9F$$
$$F$$
Explanation
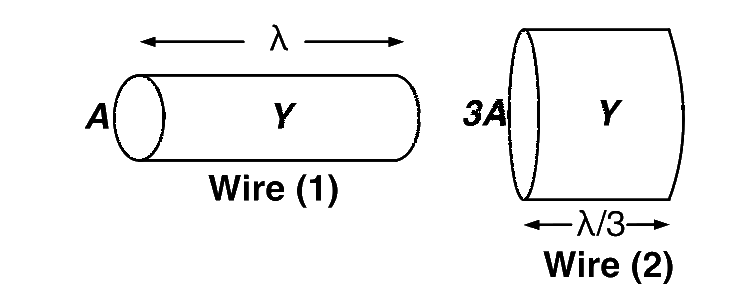
As shown in the figure, the wires will have the same Young's modulus (same material) and the length of the wire of area of cross-section $$3A$$ will be $$\ell /3$$ (same volume as wire $$1$$).
For wire $$1,$$
$$y = {{F/A} \over {\Delta x/\ell }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...(i)$$
For wire $$2.$$
$$Y = {{F'/3A} \over {\Delta x/\left( {\ell /3} \right)}}........(ii)$$
From $$(i)$$ and $$(ii),$$ $${F \over A} \times {\ell \over {\Delta x}} = {{F'} \over {3A}} \times {\ell \over {3\Delta x}} \Rightarrow F' = 9F$$
Comments (0)


