JEE MAIN - Physics (2009 - No. 7)
A transparent solid cylindrical rod has a refractive index of $${2 \over {\sqrt 3 }}.$$ It is surrounded by air. A light ray is incident at the mid-point of one end of the rod as shown in the figure.
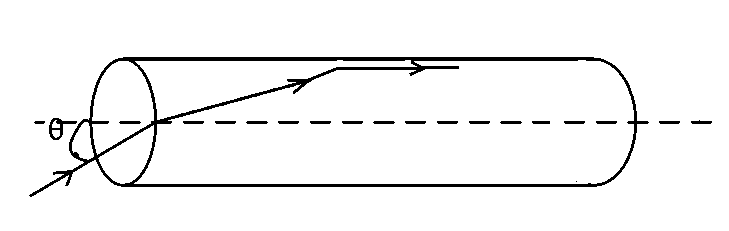

The incident angle $$\theta $$ for which the light ray grazes along the wall of the rod is :
$${\sin ^{ - 1}}\left( {{\raise0.5ex\hbox{$\scriptstyle {\sqrt 3 }$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}} \right)$$
$${\sin ^{ - 1}}\left( {{\raise0.5ex\hbox{$\scriptstyle 2$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle {\sqrt 3 }$}}} \right)$$
$${\sin ^{ - 1}}\left( {{1 \over {\sqrt 3 }}} \right)$$
$${\sin ^{ - 1}}\left( {{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}} \right)$$
Explanation
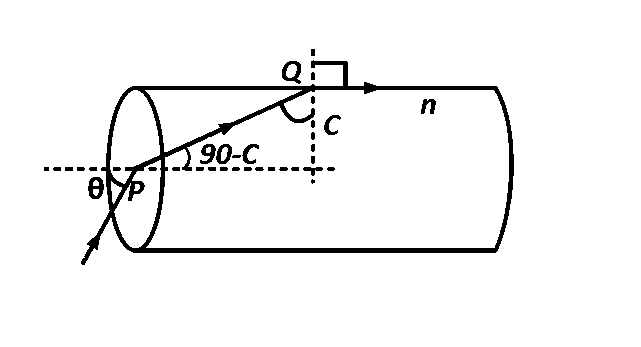
Applying Snell's law at $$Q$$
$$n = {{\sin {{90}^ \circ }} \over {\sin C}} = {1 \over {\sin C}}$$
$$\therefore$$ $$\sin C = {1 \over n} = {{\sqrt 3 } \over 2}$$
$$\therefore$$ $$C = {60^ \circ }$$
Applying Snell's Law at $$P$$
$$n = {{\sin \theta } \over {\sin \left( {90 - C} \right)}}$$
$$ \Rightarrow \sin \theta = n \times \sin \left( {90 - C} \right);$$ from $$(1)$$
$$ \Rightarrow \sin \theta = n\,\cos C$$
$$\therefore$$ $$\theta = {\sin ^{ - 1}}\left[ {{2 \over {\sqrt 3 }} \times \cos {{60}^0}} \right]$$
or, $$\theta = {\sin ^{ - 1}}\left( {{1 \over {\sqrt 3 }}} \right)$$
Comments (0)


