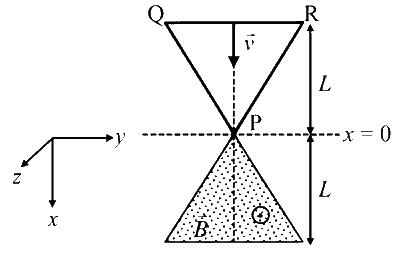
$x-y$ समतल में स्थित $L$ ऊंचाई के एक समबाहु त्रिभुजाकार क्षेत्र के अन्दर, $+z$-दिशा में एकसमान चुम्बकीय क्षेत्र $\vec{B}$ है। इसी $x-y$ समतल पर उसी $L$ ऊंचाई के एक समबाहु त्रिभुजाकार चालक लूप $\mathrm{PQR}$ को रखा है जिसका $\mathrm{P}$ शीर्ष, चित्र में दिखाए गये अभिविन्यास के अनुसार, $x=0$ पर है। समय $t=0$ पर, लूप, $+x$-दिशा में एकसमान वेग $\vec{v}$ से चुम्बकीय क्षेत्र में प्रवेश करना प्रारम्भ करता है। इस गति के दौरान लूप का तल और अभिविन्यास (orientation) अपरिवर्तित रहते हैं।

निम्न में से कौन सा ग्राफ, $x=0$ से प्रारंभ करते हुए, लूप में उत्पन्न हुए विद्युत वाहक बल $(E)$ का दूरी $(x)$ के साथ फलन, सबसे उचित रूप से दर्शाता है?

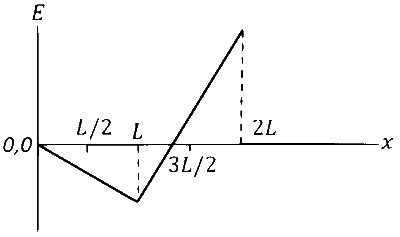
द्रव्यमान $m$ का एक कण द्रव्यमान $M(\gg m)$ के एक पिंड के गुरुत्वाकर्षण क्षेत्र के प्रभाव में है। यह कण $r_0$ त्रिज्या की एक वृत्ताकार कक्षा में $M$ के परितः आवर्तकाल $T_0$ से परिक्रमण कर रहा है। अब कण पर एक अतिरिक्त केन्द्रीय बल, जिसके संगत स्थितिज ऊर्जा $V_c(r)=m \alpha / r^3$ है, लगाया जाता है, जहाँ $\alpha$ एक धनात्मक नियतांक है तथा $r$ उसी कक्षा के केंद्र से दूरी है। यदि कण अब उसी त्रिज्या $r_0$ की कक्षा में $M$ तथा $V_{\mathrm{c}}(r)$ के संयुक्त विभव के अंतर्गत एक नए आवर्तकाल $T_1$ से परिक्रमण करता है तो, $\left(T_1^2-T_0^2\right) / T_1^2$ का मान है,

[ $G$ गुरुत्वीय नियतांक है।]

परमाणु क्रमांक (atomic number) $Z=46$ के धातु के एक लक्ष्य (target) पर उच्च ऊर्जा का एक इलेक्ट्रान पुंज प्रहार करता है। इस लक्ष्य से उत्पन्न X-किरणों का विश्लेषण किया जाता है। इससे $K_\alpha$-रेखा तथा अंतक (cut-off) तरंगदैर्घ्यों का अनुपात $r=2$ पाया जाता है। वही इलेक्ट्रान पुंज यदि $z=41$ की एक दूसरी धातु के लक्ष्य पर प्रहार करे, तो $r$ का मान होगा

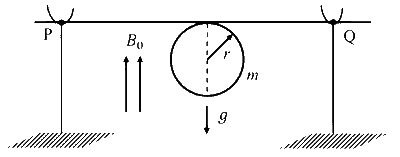
विद्युतरोधी परत चढ़े एक धातु के पतले एवं कड़े तार को मोड़कर एक वृत्ताकार वलय बनाया जाता है, जिसके दो सिरे वलय के ही एक बिंदु से उसकी स्पर्श रेखीय दिशा में सीधे निकले हैं। इस वलय का द्रव्यमान $m$ तथा त्रिज्या $r$ है तथा यह एक ऊर्ध्वाधर दिशा में ऊपर की ओर लगे एकसमान चुम्बकीय क्षेत्र $B_0$ में, चित्रानुसार, है| आरम्भ में यह तार दो दृढ चालक स्तंभों, $\mathrm{P}$ और $\mathrm{Q}$, पर गुरुत्वीय त्वरण $\mathrm{g}$ के कारण ऊर्ध्वाधर लटक रहा है| जब वलय में धारा $I$ प्रवाहित की जाती है तो वलय, रेखा $\mathrm{PQ}$ के परितः, निम्नप्रकार दिए कोण $\theta$ से घूम जाएगा

एक सूक्ष्म विद्युत्त द्विध्रुव $\vec{p}_0$ जिसका अपने केंद्र के परितः जड़त्व आघूर्ण $I$ है, को त्रिज्या $R$ की एक गोलीय सतह के केंद्र से $r$ दूरी पर रखा गया है। इस गोलीय सतह पर एकसमान क्षेत्रीय आवेश घनत्व $\sigma$ है| इस द्विध्रुव को आरम्भ में चित्रानुसार एक सूक्ष्म कोण $\theta$ पर रखा है। यह द्विध्रुव दूरी $r$ पर स्थिर रहते हुए अपने केंद्र के परितः घूर्णन के लिए स्वतंत्र है।

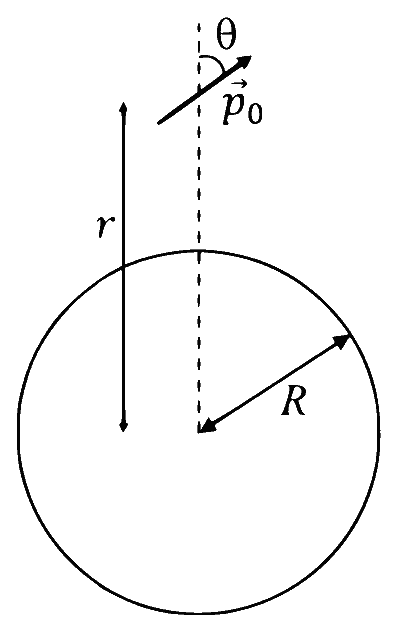
यदि इसे स्थिर अवस्था से छोड़ा जाता है तो निम्न में से कौन सा/से कथन सही है हैं)?

[ $\varepsilon_0$ मुक्त आकाश की विद्युतशीलता है।]

टेबल टेनिस की एक गेंद की त्रिज्या $(3 / 2) \times 10^{-2} \mathrm{~m}$ तथा द्रव्यमान $(22 / 7) \times 10^{-3} \mathrm{~kg}$ है। इसे एक तरण ताल (swimming pool) में धीरे-धीरे पानी की सतह से गहराई $d=0.7 \mathrm{~m}$ तक ले जाकर स्थिर अवस्था से छोड़ते हैं। यह गेंद, बिना पानी से भीगे हुए, पानी की सतह से चाल $v$ से बाहर आती है और ऊंचाई $H$ तक जाती है। निम्न में से कौन सा/से विकल्प सही है(हैं)?

[दिया है: $\pi=22 / 7, g=10 \mathrm{~ms}^{-2}$, पानी का घनत्व $=1 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3}$, पानी की श्यानता (viscosity) $=1 \times 10^{-3} \mathrm{~Pa}-\mathrm{s}$ ]

द्रव्यमान संख्या $A_{\mathrm{M}}$ के एक धनात्मक एकल आयनित (singly ionized) परमाणु को विरामावस्था से, विभवान्तर $192 \mathrm{~V}$ द्वारा त्वरित किया जाता है जिसके बाद वह एक चुम्बकीय क्षेत्र, $\vec{B}_0=0.1 \hat{k}$ Tesla, युक्त $w$ चौड़ाई के एक आयताकार क्षेत्र में, चित्रानुसार प्रवेश करता है। अंततः यह आयन एक संसूचक (detector) पर अपने आरंभिक पथ से नीचे दूरी $x$ पर टकराता है।

[दिया है: न्यूट्रॉन/प्रोटोन का द्रव्यमान $=(5 / 3) \times 10^{-27} \mathrm{~kg}$, इलेक्ट्रान का आवेश $=1.6 \times 10^{-19} \mathrm{C}$ ]

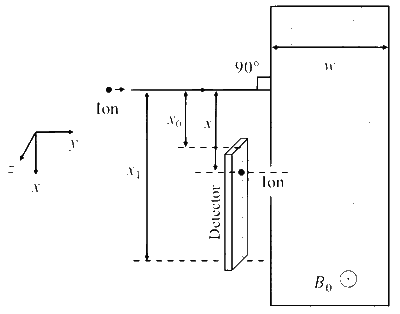
निम्न में से कौन सा/से विकल्प सही है (हैं)?

एक शंकु की विमायें अल्पत्मांक $2 \mathrm{~mm}$ के एक पैमाने से मापे जाने पर उसके आधार का व्यास तथा ऊँचाई, दोनों, $20.0 \mathrm{~cm}$ पाये जाते हैं| इस शंकु का आयतन ज्ञात करने में अधिकतम प्रतिशत त्रुटि का मान ________ होगा|

क्षैतिज खेल के मैदान के एक बिंदु $\left(x_0, y_0\right)=(0,0)$ से एक गेंद $+x$-दिशा से $\theta_0$ कोण पर प्रारंभिक चाल $v_0$ से फेंकी जाती है| गेंद को एक पत्थर से टकराना है जो उसी क्षण बिंदु $\left(x_1, y_1\right)=(L, 0)$ से फेंका जाता है। पत्थर को उचित प्रारंभिक चाल से एवं $+x$-दिशा से $\left(180-\theta_1\right)$ के कोंण पर फेंका जाता है। एक नियत $v_0$ के लिए, जब $\left(\theta_0, \theta_1\right)=\left(45^{\circ}, 45^{\circ}\right)$, तो पत्थर $T_1$ समय पश्चात, तथा जब $\left(\theta_0, \theta_1\right)=\left(60^{\circ}, 30^{\circ}\right)$, तो पत्थर $T_2$ समय पश्चात्, गेंद से टकराता है। इस दशा में $\left(T_1 / T_2\right)^2$ ______ है।

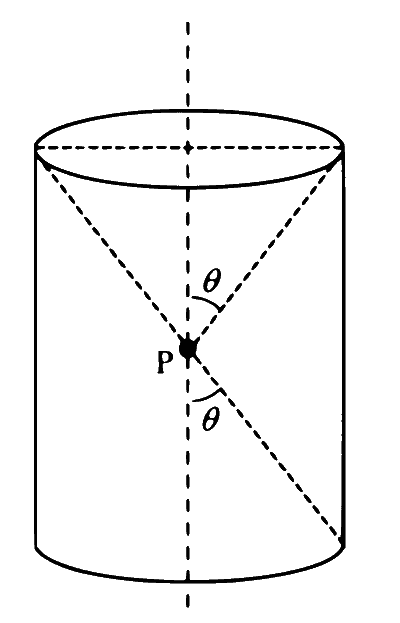
एक आवेश को एक बेलनाकार क्षेत्र के केंद्र बिंदु $\mathrm{P}$ पर चित्रानुसार रखा गया है जिससे बेलन के दो छोर, बिंदु $\mathrm{P}$ पर $\theta$ अर्ध-कोण अंतरित करते हैं। जब $\theta=30^{\circ}$ तो बेलन के बेलनाकार पृष्ठ से विद्युत फ्लक्स (flux) $\Phi$ है। यदि $\theta=60^{\circ}$ तो बेलनाकार पृष्ठ से विद्युत फ्लक्स $\Phi / \sqrt{n}$ है, जहाँ $n$ का मान ________ है।

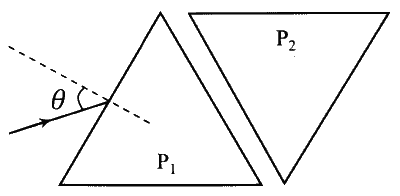
दो समबाहु त्रिभुजाकार प्रिज्मों, $P_1$ एवं $P_2$ को एक दूसरे की भुजाओं के समानांतर, निर्वात में चित्रानुसार रखा गया है। प्रकाश की एक किरण, प्रिज्म $\mathrm{P}_1$ पर आपतन कोण $\theta$ से इस तरह से आपतित होती है कि बाहर जाती हुयी किरण का प्रिज्म $P_2$ द्वारा अल्पतम विचलन (minimum deviation) होता है। यदि $P_1$ एवं $P_2$ के अपवर्तनांक, क्रमशः, $\sqrt{\frac{3}{2}}$ तथा $\sqrt{3}$ हैं, तो $\theta=\sin ^{-1}\left[\sqrt{\frac{3}{2}} \sin \left(\frac{\pi}{\beta}\right)\right]$ है, जहाँ $\beta$ का मान ________ है।

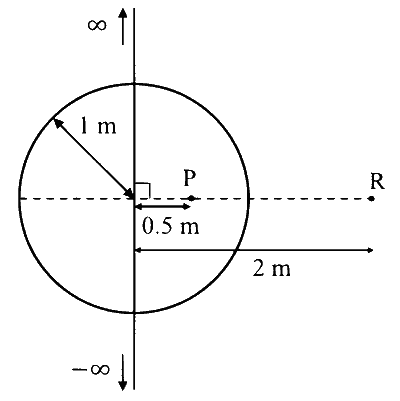
अनंत लम्बाई का एक पतला तार, जिसका एकसमान रेखीय आवेश घनत्व $5 ~\mathrm{nC} / \mathrm{m}$ है, को $1 \mathrm{~m}$ त्रिज्या की एक गोलीय सतह को भेदकर, चित्रानुसार रखा है| गोलीय सतह पर $10 ~\mathrm{nC}$ आवेश एकसमान रूप से वितरित है। यदि आवेशों का अभिविन्यास स्थैतिक है, तो बिंदुओं $P$ तथा $R$ के बीच के विभवान्तर का वोल्ट में परिमाण __________ होगा|

[दिया है: SI इकाई में $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9, \ln 2=0.7$; तार द्वारा छेदित क्षेत्र नगण्य मानिये|]

दाब $\mathrm{P}_0=10^5 \mathrm{~Pa}$ के एक वायु कोष्ठ (air chamber) के अन्दर किसी त्रिज्या का साबुन का एक गोलाकार बुलबुला है जिसके अन्दर अतिरिक्त दाब (excess pressure) $\Delta \mathrm{P}=144 \mathrm{~Pa}$ है। अब कोष्ठ का दाब घटाकर $8 \mathrm{P}_0 / 27$ कर दिया जाता है जिससे बुलबुले की त्रिज्या तथा अतिरिक्त दाब बदल जाते हैं। इस प्रक्रिया में सभी तापमान अपरिवर्तित रहते हैं। वायु को आदर्श गैस मानिये तथा दोनों स्थितियों में अतिरिक्त दाब $\Delta \mathrm{P}$ का मान कोष्ठ दाब से नगण्य मानिये| नए अतिरिक्त दाब $\Delta \mathrm{P}$ का $\mathrm{Pa}$ में मान _______ होगा|

बिंदु $O$ से ऊपर आठवीं 8^th दीप्त फ्रिंज, दो चरम स्थितियों के बीच, समय के साथ दोलन करती है। इन दोनों चरम स्थितियों के बीच की दूरी माइक्रो मीटर $(\mu \mathrm{m})$ में _______ होगी|

आठवीं ( $\left.8^{\mathrm{th}}\right)$ दीप्त फ्रिंज के चलने की अधिकतम चाल ________ $\mu \mathrm{m} / \mathrm{s}$ होगी

यदि संघट्ट, समय $t_0=0$ पर होता है तो $v_{\mathrm{cm}} /(a \omega)$ का मान _________ होगा|

यदि संघट्ट, समय $t_0=\pi /(2 \omega)$ पर होता है तो $4 b^2 / a^2$ का मान _________ होगा|