JEE Advance - Physics Hindi (2024 - Paper 2 Online - No. 5)
एक सूक्ष्म विद्युत्त द्विध्रुव $\vec{p}_0$ जिसका अपने केंद्र के परितः जड़त्व आघूर्ण $I$ है, को त्रिज्या $R$ की एक गोलीय सतह के केंद्र से $r$ दूरी पर रखा गया है। इस गोलीय सतह पर एकसमान क्षेत्रीय आवेश घनत्व $\sigma$ है| इस द्विध्रुव को आरम्भ में चित्रानुसार एक सूक्ष्म कोण $\theta$ पर रखा है। यह द्विध्रुव दूरी $r$ पर स्थिर रहते हुए अपने केंद्र के परितः घूर्णन के लिए स्वतंत्र है।
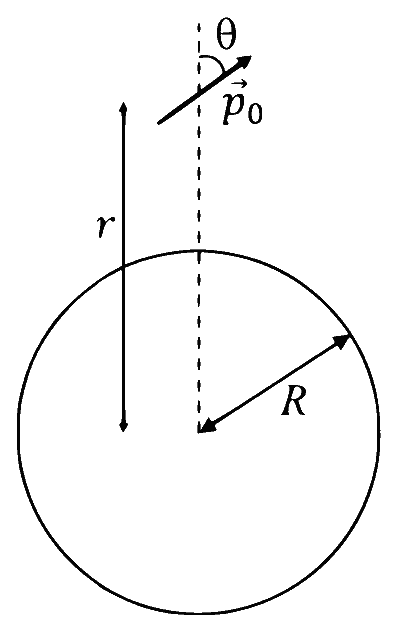
यदि इसे स्थिर अवस्था से छोड़ा जाता है तो निम्न में से कौन सा/से कथन सही है हैं)?
[ $\varepsilon_0$ मुक्त आकाश की विद्युतशीलता है।]
किसी भी परिमित दूरी $r$ पर द्विध्रुव लघु दोलन (small oscillations) करेगा|
किसी भी परिमित दूरी $r>R$ के लिए द्विध्रुव लघु दोलन करेगा|
यदि $r=2 R$ हो तो द्विध्रुव $\sqrt{\frac{2 \sigma p_0}{\epsilon_0 I}}$ कोणीय आवृत्ति से लघु दोलन करेगा।
यदि $r=10 R$ हो तो द्विध्रुव $\sqrt{\frac{\sigma p_0}{100 \epsilon_{0}!}}$ कोणीय आवृत्ति से लघु दोलन करेगा|
Comments (0)


