JEE Advance - Physics Hindi (2024 - Paper 2 Online - No. 17)
एक द्रव्यमानरहित स्प्रिंग से जुड़े एक ही द्रव्यमान $m$ के दो कण, 1 और 2 , चित्रानुसार एक घर्षण रहित समतल पर हैं| प्रारंभ में, ये दोनों कण, जिनका द्रव्यमान केंद्र $x_0$ पर है, आयाम $a$ तथा कोणीय आवृति $\omega$ से दोलन कर रहे हैं। अतः, समय $t$ पर उनकी स्थितियां, क्रमशः, $x_1(t)=\left(x_0+d\right)+a \sin \omega t$ और $x_2(t)=\left(x_0-d\right)-a \sin \omega t$ हैं, जहां $d>2 a$ है। द्रव्यमान $m$ का एक कण 3 , चाल $u_0=a \omega / 2$ से इस निकाय की तरफ चलते हुए समय $t_0$ पर कण 2 से तात्क्षणिक प्रत्यास्थ संघट्ट (elastic collision) करता है| अंततः, कणों 1 व 2 का द्रव्यमान-केंद्र चाल $v_{\mathrm{cm}}$ से चलता है और ये कण आयाम $b$ तथा उसी कोणीय आवृति $\omega$ से दोलन करते हैं।
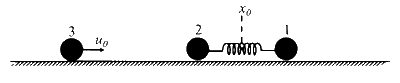
एक द्रव्यमानरहित स्प्रिंग से जुड़े एक ही द्रव्यमान $m$ के दो कण, 1 और 2 , चित्रानुसार एक घर्षण रहित समतल पर हैं| प्रारंभ में, ये दोनों कण, जिनका द्रव्यमान केंद्र $x_0$ पर है, आयाम $a$ तथा कोणीय आवृति $\omega$ से दोलन कर रहे हैं। अतः, समय $t$ पर उनकी स्थितियां, क्रमशः, $x_1(t)=\left(x_0+d\right)+a \sin \omega t$ और $x_2(t)=\left(x_0-d\right)-a \sin \omega t$ हैं, जहां $d>2 a$ है। द्रव्यमान $m$ का एक कण 3 , चाल $u_0=a \omega / 2$ से इस निकाय की तरफ चलते हुए समय $t_0$ पर कण 2 से तात्क्षणिक प्रत्यास्थ संघट्ट (elastic collision) करता है| अंततः, कणों 1 व 2 का द्रव्यमान-केंद्र चाल $v_{\mathrm{cm}}$ से चलता है और ये कण आयाम $b$ तथा उसी कोणीय आवृति $\omega$ से दोलन करते हैं।

एक द्रव्यमानरहित स्प्रिंग से जुड़े एक ही द्रव्यमान $m$ के दो कण, 1 और 2 , चित्रानुसार एक घर्षण रहित समतल पर हैं| प्रारंभ में, ये दोनों कण, जिनका द्रव्यमान केंद्र $x_0$ पर है, आयाम $a$ तथा कोणीय आवृति $\omega$ से दोलन कर रहे हैं। अतः, समय $t$ पर उनकी स्थितियां, क्रमशः, $x_1(t)=\left(x_0+d\right)+a \sin \omega t$ और $x_2(t)=\left(x_0-d\right)-a \sin \omega t$ हैं, जहां $d>2 a$ है। द्रव्यमान $m$ का एक कण 3 , चाल $u_0=a \omega / 2$ से इस निकाय की तरफ चलते हुए समय $t_0$ पर कण 2 से तात्क्षणिक प्रत्यास्थ संघट्ट (elastic collision) करता है| अंततः, कणों 1 व 2 का द्रव्यमान-केंद्र चाल $v_{\mathrm{cm}}$ से चलता है और ये कण आयाम $b$ तथा उसी कोणीय आवृति $\omega$ से दोलन करते हैं।

Comments (0)


