JEE Advance - Physics (2017 - Paper 2 Offline)
2
Two coherent monochromatic point sources $${S_1}$$ and $${S_2}$$ of wavelength $$\lambda = 600\,nm$$ are placed symmetrically on either side of the center of the circle as shown. The sources are separated by a distance $$d=1.8$$ $$mm.$$ This arrangement produces interference fringes visible as alternate bright and dark spots on the circumference of the circle. The angular separation between two consecutive bright spots is $$\Delta \theta .$$ Which of the following options is/are correct?


Answer
B
D
3
The instantaneous voltages at three terminals marked $$X,Y$$ and $$Z$$ are given by
$${V_x} = {V_0}\,\sin \,\omega t,$$
$${V_Y} = {V_0}\,\sin $$ $$\left( {\omega t + {{2\pi } \over 3}} \right)$$
and $$Vz = {V_0}\sin \left( {\omega t + {{4\pi } \over 3}} \right)$$
An ideal voltmeter is configured to read $$rms$$ value of the potential difference between its terminals. It is connected between points $$X$$ and $$Y$$ and then between $$Y$$ and $$Z.$$ The reading(s) of the voltmeter will be
$${V_x} = {V_0}\,\sin \,\omega t,$$
$${V_Y} = {V_0}\,\sin $$ $$\left( {\omega t + {{2\pi } \over 3}} \right)$$
and $$Vz = {V_0}\sin \left( {\omega t + {{4\pi } \over 3}} \right)$$
An ideal voltmeter is configured to read $$rms$$ value of the potential difference between its terminals. It is connected between points $$X$$ and $$Y$$ and then between $$Y$$ and $$Z.$$ The reading(s) of the voltmeter will be
Answer
A
D
4
A uniform magnetic field $$B$$ exist in the region between $$x=0$$ and $$x = {{3R} \over 2}$$ (region $$2$$ in the figure) pointing normally into the plane of the paper. A particle with charge $$+Q$$ and momentum $$p$$ directed along $$x$$-axis enters region $$2$$ from region $$1$$$ at point $${P_1}\left( y \right) = - R).$$ Which of the following option(s) is/are correct?
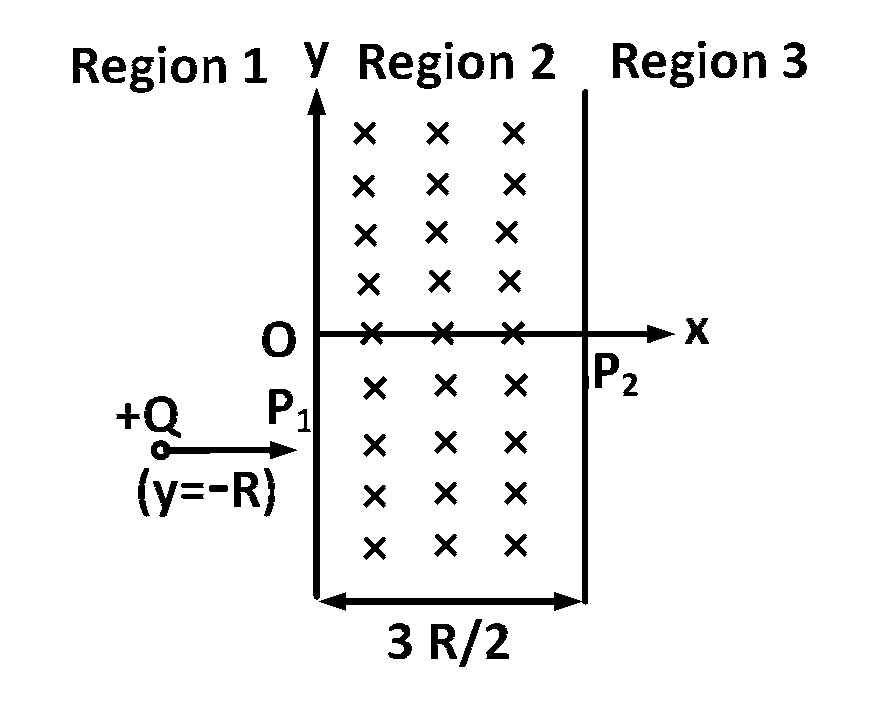

Answer
A
B
5
A person measures the depth of a well by measuring the time interval between dropping a stone and receiving the sound of impact with the bottom of the well. The error in his measurement of time is $$\delta T = 0.01$$ seconds and he measures the depth of the well to be $$L=20$$ meters. Take the acceleration due to gravity $$g = 10m{s^{ - 2}}$$ and the velocity of sound is $$300$$ $$m{s^{ - 1}}$$. Then the fractional error in the measurement, $$\delta L/L,$$ is closest to
Answer
(B)
$$1\% $$
6
A rocket is launched normal to the surface of the Earth, away from the sun, along the line joining the Sun and the Earth. The Sun is $$3 \times 10{}^5$$ times heavier than the earth and is at a distance $$2.5 \times {10^4}$$ times larger than the radius of the Earth. The escape velocity from Earth's gravitational field is $${V_c} = 11.2km\,{s^{ - 1}}.$$. The minimum initial velocity $$\left( {{v_s}} \right)$$ required for the rocket to be able to leave the sun-earth system is closest to (Ignore the the rotation and revoluation of the earth and the presence of any other planet)
Answer
(B)
$${v_s} = 42\,km\,{s^{ - 1}}$$
7
Three vectors $$\overrightarrow P ,\overrightarrow Q $$ and $$\overrightarrow R $$ are shown in the figure. Let $$S$$ be any point on the vector $$\overrightarrow R .$$ The distance between the points $$P$$ and $$S$$ is $$b\left| {\overrightarrow R } \right|.$$ The general relation among vectors $$\overrightarrow P ,\overrightarrow Q $$ and $$\overrightarrow S $$ is :


Answer
(A)
$$\overrightarrow S = \left( {1 - b} \right)\overrightarrow P + b\overrightarrow Q $$
8
Consider regular polygons with number of sides $$n=3,4,5....$$ as shown in the figure. The center of mass of all the polygons is at height $$h$$ from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted. The maximum increase in height of the locus of the center of mass for each polygon is $$\Delta $$. Then $$\Delta $$ depends on $$n$$ and $$h$$ as
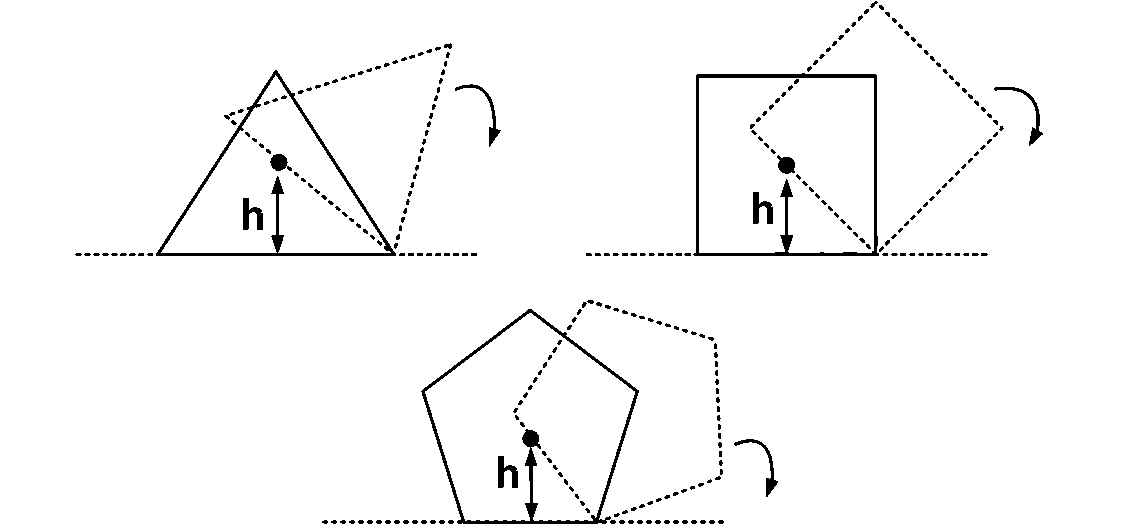

Answer
(B)
$$\Delta = h\left( {{1 \over {\cos \left( {{\pi \over n}} \right)}} - 1} \right)$$
9
A symmetric star shaped conducting wire loop is carrying a steady state current $${\rm I}$$ as shown in the figure. The distance between the diametrically opposite vertices of the star is $$4a.$$ The magnitude of the magnetic field at the center of the loop is


Answer
(A)
$${{{\mu _0}1} \over {4\pi a}}6\left[ {\sqrt 3 - 1} \right]$$
10
A photoelectric material having work-function $${\phi _0}$$ is illuminated with light of wavelength $$\lambda \left( {\lambda < {{he} \over {{\phi _0}}}} \right).$$ The fastest photoelectron has a de-Broglic wavelength $${\lambda _d}.$$ A change in wavelength of the incident light by $$\Delta \lambda $$ result in a change $$\Delta {\lambda _d}$$ in $${\lambda _d}.$$ Then the ratio $$\Delta {\lambda _d}/\Delta \lambda $$ is proportional to
Answer
(D)
$$\lambda _d^3/{\lambda ^2}$$
11
Consider regular polygons with number of sides $$n=3,4,5....$$ as shown in the figure. The center of mass of all the polygons is at height $$h$$ from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted. The maximum increase in height of the locus of the center of mass for each polygon is $$\Delta $$. Then $$\Delta $$ depends on $$n$$ and $$h$$ as


Answer
(B)
$$\Delta = h\left( {{1 \over {\cos \left( {{\pi \over n}} \right)}} - 1} \right)$$
12
Consider an expanding sphere of instantaneous radius R whose total mass remains constant. The expansion is such that the instantaneous density $$\rho $$ remains uniform throughout the volume. The rate of fractional change in density $$\left( {{1 \over \rho } {{d\rho } \over {dt}}} \right)$$ is constant. The velocity $$v$$ of any point on the surface of the expanding sphere is proportional to
Answer
(A)
$$R$$
14
A source of constant voltage V is connected to a resistance R and two ideal inductors L1 and L2 through a switch S as shown. There is no mutual inductance between the two inductors. The switch S is initially open. At t = 0, the switch is closed and current begins to flow. Which of the following options is/are correct?


Answer
A
B
C



