Sign In

JEE Advance - Physics (2017 - Paper 2 Offline - No. 4)

A uniform magnetic field $$B$$ exist in the region between $$x=0$$ and $$x = {{3R} \over 2}$$ (region $$2$$ in the figure) pointing normally into the plane of the paper. A particle with charge $$+Q$$ and momentum $$p$$ directed along $$x$$-axis enters region $$2$$ from region $$1$$$ at point $${P_1}\left( y \right) = - R).$$ Which of the following option(s) is/are correct?

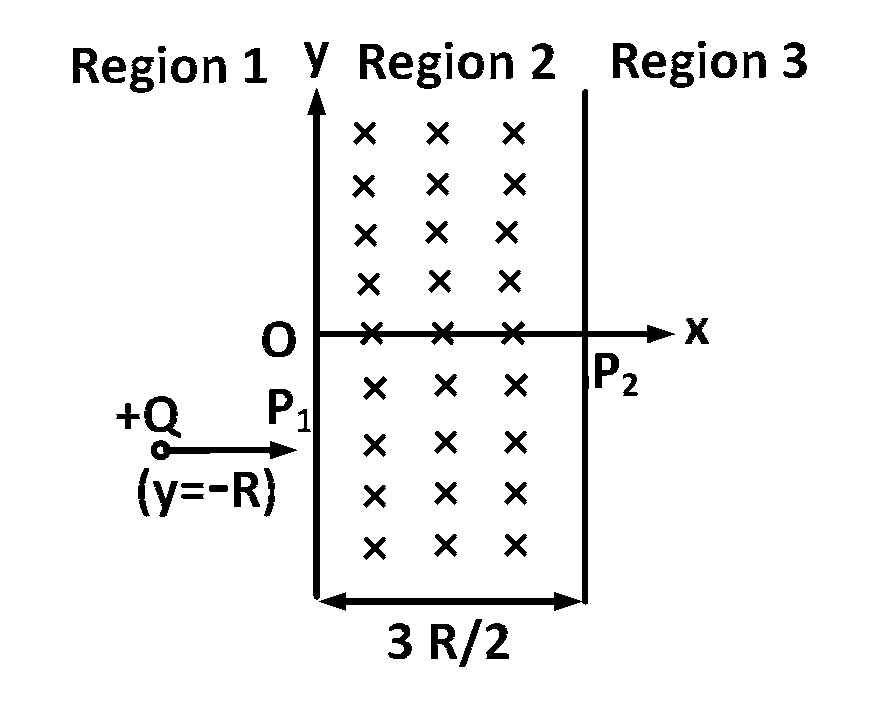
JEE Advanced 2017 Paper 2 Offline Physics - Magnetism Question 39 English
For $$B > {2 \over 3}{p \over {QR}}$$ the particle well re-enter region $$1$$
For $$B = {8 \over {13}}{p \over {QR}},$$ the particle will enter region $$3$$ through the point $${P_2}$$ on $$x$$-axis
When the particle re-enters region $$1$$ through the longest possible path in region $$2,$$ the magnitude of the change in its linear momentum between point $${P_1}$$ and the farthest point from $$y$$-axis is $$p/\sqrt 2 $$
For a fixed $$B,$$ particles of same charge $$Q$$ and same velocity $$v,$$ the distance between the point $${P_1}$$ and the point of re-entry into region $$1$$ is inversely proportional to the mass of the particle

Explanation

As the magnetic field is perpendicular to motion of particle.

$$\therefore$$ Particle will move in curved path of radius,

$$r = {{mv} \over {QB}} = {p \over {QB}}$$ ($$\because$$ p = mv)

Particle will cross the region 2 if

$$r > {{3R} \over 2} \Rightarrow B < {{2p} \over {3QR}}$$

and particle will re-enter region 1 if

$$r < {{3R} \over 2} \Rightarrow B > {{2p} \over {3QR}}$$

JEE Advanced 2017 Paper 2 Offline Physics - Magnetism Question 39 English Explanation 1

Here a = 0, b = (r $$-$$ R)

Equation of trajectory, $${(x - a)^2} + {(y - b)^2} = {r^2}$$

$$\therefore$$ To pass through region 2, at $${P_2}\left( {{{3R} \over 2},0} \right)$$,

$${\left( {{{3R} \over 2}} \right)^2} + {(r - R)^2} = {r^2}$$ or $${9 \over 4}{R^2} + {r^2} + {R^2} - 2rR = {r^2}$$

$${{13} \over 4}{R^2} = 2rR$$ or $$r = {{13} \over 8}R \Rightarrow {p \over {QB}} = {{13} \over 8}R$$ or $$B = {8 \over {13}}{p \over {QR}}$$

Hence, for $$B = {8 \over {13}}{p \over {QR}}$$ particle will enter region 3 through P2

For $$r < {{3R} \over 2}$$, particle will re-enter region 1 through point P3(x, y).

$$y = (2r - R) = \left( {{{2mv} \over {QB}} - R} \right)$$, x = 0

$$\Rightarrow$$ y $$\propto$$ m

JEE Advanced 2017 Paper 2 Offline Physics - Magnetism Question 39 English Explanation 2

At farthest point from y-axis, the momentum is perpendicular to initial momentum.

$$\therefore$$ $$\Delta p = \sqrt 2 mv = \sqrt 2 p$$

Comments (0)

Advertisement