JEE Advance - Physics (2017 - Paper 2 Offline - No. 13)
A rigid uniform bar AB of length L is slipping from its vertical position on a frictionless floor (as shown in the figure). At some instant of time, the angle made by the bar with the vertical is $$\theta$$. Which of the following statements about its motion is/are correct?


Instantaneous torque about the point in contact with the floor is proportional to sin$$\theta$$
The trajectory of the point A is parabola
The mid-point of the bar will fall vertically downward
When the bar makes an angle $$\theta$$ with the vertical, the displacement of its mid-point from the initial position is proportional to (1 $$-$$ cos$$\theta$$)
Explanation
We discuss the options as follows:
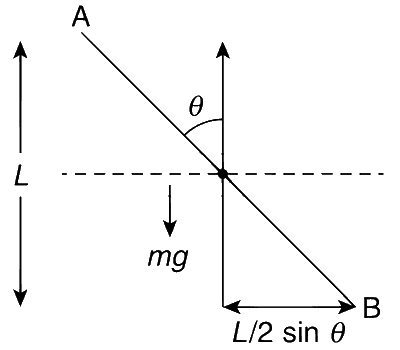
$$\bullet$$ For option (A) : When the bar makes an angle $$\theta$$ with the floor, the height of the midpoint is $${L \over 2}\cos \theta $$. this is height of centre of mass.
A force mg acts vertically downward. Thus, the midpoint of bar falls vertically downward. Hence, option (A) is correct.
$$\bullet$$ For option (B) : Here, we have $$x = {L \over 2}\sin \theta $$ and $$y = L\cos \theta $$; therefore,
$$\sin \theta = {x \over {L/2}}$$ and $$\cos \theta = {y \over L}$$
Using the condition $${\sin ^2}\theta + {\cos ^2}\theta = 1$$, we get
$${{{x^2}} \over {{{(L/2)}^2}}} + {{{y^2}} \over {{L^2}}} = 1$$ (equation of ellipse)
Thus, trajectory of point A is not parabola. Hence, option (B) is incorrect.
$$\bullet$$ For option (C) : The torque acting about the point of contact with floor, that is, at point B is
$$\tau = \overrightarrow F \times \overrightarrow r = mg{L \over 2}\sin \theta $$
Thus, the torque is proportional to sin$$\theta$$. Hence, option (C) is correct.
$$\bullet$$ For option (D) : The displacement of midpoint is
$${L \over 2} - {L \over 2}\cos \theta = {L \over 2}(1 - \cos \theta )$$
That is,
Displacement $$\propto$$ (1 $$-$$ cos$$\theta$$)
Hence, option (D) is correct.

$$\bullet$$ For option (A) : When the bar makes an angle $$\theta$$ with the floor, the height of the midpoint is $${L \over 2}\cos \theta $$. this is height of centre of mass.
A force mg acts vertically downward. Thus, the midpoint of bar falls vertically downward. Hence, option (A) is correct.
$$\bullet$$ For option (B) : Here, we have $$x = {L \over 2}\sin \theta $$ and $$y = L\cos \theta $$; therefore,
$$\sin \theta = {x \over {L/2}}$$ and $$\cos \theta = {y \over L}$$
Using the condition $${\sin ^2}\theta + {\cos ^2}\theta = 1$$, we get
$${{{x^2}} \over {{{(L/2)}^2}}} + {{{y^2}} \over {{L^2}}} = 1$$ (equation of ellipse)
Thus, trajectory of point A is not parabola. Hence, option (B) is incorrect.
$$\bullet$$ For option (C) : The torque acting about the point of contact with floor, that is, at point B is
$$\tau = \overrightarrow F \times \overrightarrow r = mg{L \over 2}\sin \theta $$
Thus, the torque is proportional to sin$$\theta$$. Hence, option (C) is correct.
$$\bullet$$ For option (D) : The displacement of midpoint is
$${L \over 2} - {L \over 2}\cos \theta = {L \over 2}(1 - \cos \theta )$$
That is,
Displacement $$\propto$$ (1 $$-$$ cos$$\theta$$)
Hence, option (D) is correct.
Comments (0)


