Sign In

JEE Advance - Physics (2017 - Paper 2 Offline - No. 8)

Consider regular polygons with number of sides $$n=3,4,5....$$ as shown in the figure. The center of mass of all the polygons is at height $$h$$ from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted. The maximum increase in height of the locus of the center of mass for each polygon is $$\Delta $$. Then $$\Delta $$ depends on $$n$$ and $$h$$ as

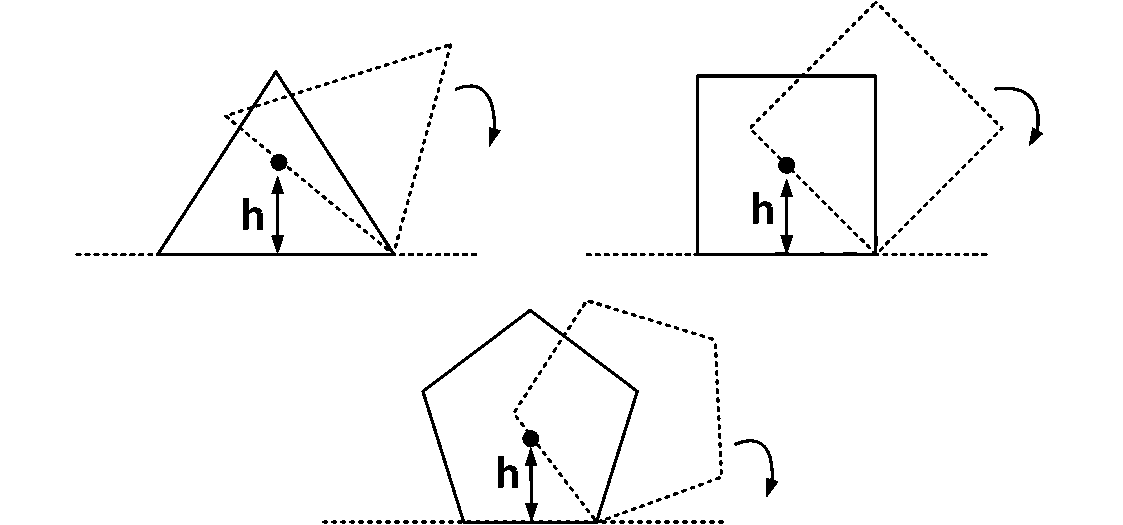
JEE Advanced 2017 Paper 2 Offline Physics - Rotational Motion Question 43 English
$$\Delta = h{\sin ^2}\left( {{\pi \over n}} \right)$$
$$\Delta = h\left( {{1 \over {\cos \left( {{\pi \over n}} \right)}} - 1} \right)$$
$$\Delta = h\sin \left( {{{2\pi } \over n}} \right)$$
$$\Delta = h\,{\tan ^2}\left( {{\pi \over {2n}}} \right)$$

Explanation

Let n be the number of sides of a regular polygon. By symmetry, its centre of mass O will be equidistant from each vertex i.e., it lies at the centre of the circumscribed circle. Let r be the radius of circumscribed circle and h be the perpendicular distance of O from any side (see figure). The angle subtended by any side on the centre O is 2$$\pi$$/n and $$\angle$$PON = $$\pi$$/n.

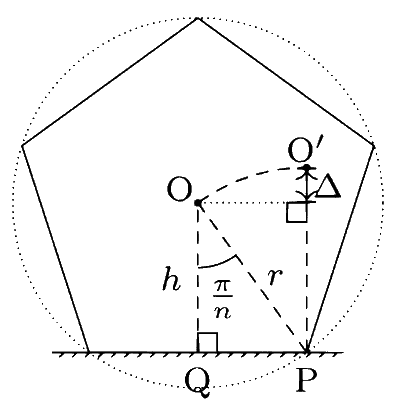
JEE Advanced 2017 Paper 2 Offline Physics - Rotational Motion Question 43 English Explanation

When polygon rolls about the vertex P (without slipping or sliding), the point O moves in a circle of radius r centred at P. The point O reaches the maximum height (point O' in the figure) when PO' is perpendicular to PQ. Thus, the maximum increase in height of the locus of the centre of mass O is given by

$$\Delta = r - h = {h \over {\cos (\pi /n)}} - h = h\left( {{1 \over {\cos (\pi /n)}} - 1} \right)$$.

Comments (0)

Advertisement