Sign In

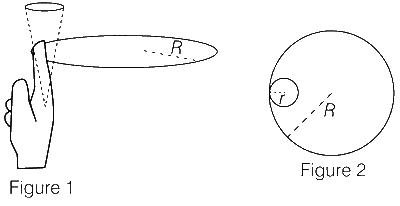
JEE Advance - Physics (2017 - Paper 2 Offline - No. 17)

One twirls a circular ring (of mass M and radius R) near the tip of one's finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is r. The finger rotates with an angular velocity $$\omega$$0. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is $$\mu$$ and the acceleration due to gravity is g.

One twirls a circular ring (of mass M and radius R) near the tip of one's finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is r. The finger rotates with an angular velocity $$\omega$$0. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is $$\mu$$ and the acceleration due to gravity is g.

One twirls a circular ring (of mass M and radius R) near the tip of one's finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is r. The finger rotates with an angular velocity $$\omega$$0. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is $$\mu$$ and the acceleration due to gravity is g.

The total kinetic energy of the ring is
$$M\omega _0^2{(R - r)^2}$$
$${1 \over 2}M\omega _0^2{(R - r)^2}$$
$$M\omega _0^2{R^2}$$
$${1 \over 2}M\omega _0^2[{(R - r)^2} + {R^2}]$$

Explanation

Let P be the contact point of the finger and the ring. The point P revolves with an angular velocity $$\omega$$0 in a circle of radius r centred at the point O (see figure). The contact point P, the centre O and the centre of the ring C are in a straight line because P is common to both the circles (i.e., circular trajectory and circular ring). Thus, the line CP will have same angular velocity as the line OP i.e., angular velocity of the line CP (or the ring) is $$\omega$$0.

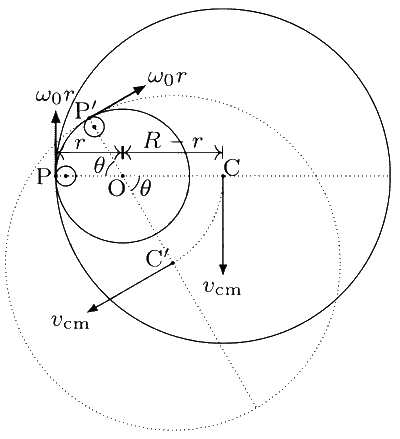
JEE Advanced 2017 Paper 2 Offline Physics - Rotational Motion Question 30 English Explanation
The velocity of the finger at the point P is $$\omega$$0r tangential to the circle in which it revolves. The ring rolls without slipping. Thus, velocity of the ring at the point P is also $$\omega$$0r tangential to the circle in which the finger revolves. Let velocity of C be vcm. Since P and C lie on the ring (a rigid body), the velocities of C and P are related by $${\overrightarrow v _C} = {\overrightarrow v _P} + \overrightarrow \omega \times \overrightarrow {PC} $$ which gives

vcm = $$\omega$$0(R $$-$$ r).

The ring rotates with an angular velocity $$\omega$$ = $$\omega$$0 and its centre of mass translates with a velocity vcm = $$\omega$$0(R $$-$$ r). Thus, kinetic energy of the ring is given by

$$K = {1 \over 2}Mv_{cm}^2 + {1 \over 2}{I_{cm}}{\omega ^2}$$

$$ = {1 \over 2}M\omega _0^2{(R - r)^2} + {1 \over 2}M{R^2}\omega _0^2$$

$$ = {1 \over 2}M\omega _0^2[{(R - r)^2} + {R^2}]$$.

Comments (0)

Advertisement