Sign In

JEE Advance - Physics (2017 - Paper 2 Offline - No. 18)

One twirls a circular ring (of mass M and radius R) near the tip of one's finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is r. The finger rotates with an angular velocity $$\omega$$0. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is $$\mu$$ and the acceleration due to gravity is g.

One twirls a circular ring (of mass M and radius R) near the tip of one's finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is r. The finger rotates with an angular velocity $$\omega$$0. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is $$\mu$$ and the acceleration due to gravity is g.

One twirls a circular ring (of mass M and radius R) near the tip of one's finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is r. The finger rotates with an angular velocity $$\omega$$0. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is $$\mu$$ and the acceleration due to gravity is g.

The minimum value of $$\omega$$0 below which the ring will drop down is
$$\sqrt {{g \over {2\mu (R - r)}}} $$
$$\sqrt {{{3g} \over {2\mu (R - r)}}} $$
$$\sqrt {{g \over {\mu (R - r)}}} $$
$$\sqrt {{{2g} \over {\mu (R - r)}}} $$

Explanation

Let the ring makes an angle $$\alpha$$ with the horizontal and the finger makes an angle $$\beta$$ with the vertical (see figure). The forces acting on the ring are its weight mg at the centre C, normal reaction N and the frictional force f at the contact point P. Resolve the forces in the horizontal and the vertical directions. The centre of mass C rotates with an angular velocity $$\omega$$0 in a horizontal circle of radius (R $$-$$ r) cos$$\alpha$$ centred at O. Apply Newton's second law in the horizontal and the vertical directions to get

$$f\cos \beta - N\sin \beta - Mg = 0$$ ..... (1)

$$N\cos \beta + f\sin \beta = M\omega _0^2(R - r)\cos \alpha $$ .... (2)

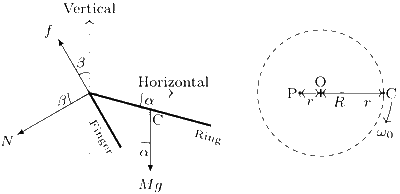
JEE Advanced 2017 Paper 2 Offline Physics - Rotational Motion Question 31 English Explanation
The minimum value of $$\omega$$0 occurs when the frictional force attains its limiting value i.e.,

$$f = \mu N$$....... (3)

Eliminate f and N from equations (1) - (3) to get

$${\omega _{0,\,\min }} = {\left[ {{{(\cos \beta + \mu \sin \beta )g} \over {(\mu \cos \beta - \sin \beta )(R - r)\cos \alpha }}} \right]^{1/2}}$$

$$ \approx {\left[ {{g \over {\mu (R - r)}}} \right]^{1/2}}$$ ($$\because$$ $$\alpha$$ = 0 and $$\beta$$ = 0).

Comments (0)

Advertisement