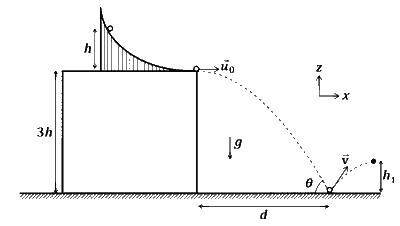
A slide with a frictionless curved surface, which becomes horizontal at its lower end, is fixed on the terrace of a building of height $3 h$ from the ground, as shown in the figure. A spherical ball of mass $m$ is released on the slide from rest at a height $h$ from the top of the terrace. The ball leaves the slide with a velocity $\vec{u}_0=u_0 \hat{x}$ and falls on the ground at a distance $d$ from the building making an angle $\theta$ with the horizontal. It bounces off with a velocity $\vec{v}$ and reaches a maximum height $h_1$. The acceleration due to gravity is $g$ and the coefficient of restitution of the ground is $1 / \sqrt{3}$. Which of the following statement(s) is(are) correct?

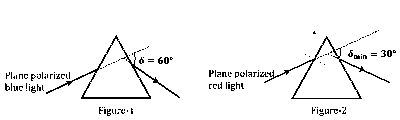
A plane polarized blue light ray is incident on a prism such that there is no reflection from the surface of the prism. The angle of deviation of the emergent ray is $\delta=60^{\circ}$ (see Figure-1). The angle of minimum deviation for red light from the same prism is $\delta_{\min }=30^{\circ}$ (see Figure-2). The refractive index of the prism material for blue light is $\sqrt{3}$. Which of the following statement(s) is(are) correct?

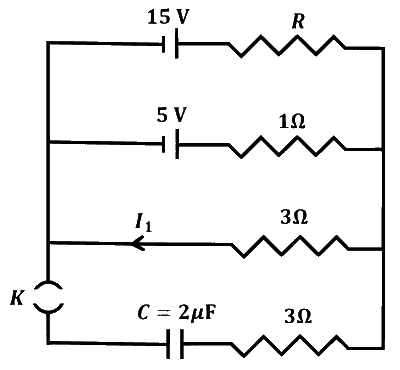
In a circuit shown in the figure, the capacitor $C$ is initially uncharged and the key $K$ is open. In this condition, a current of $1 \mathrm{~A}$ flows through the $1 \Omega$ resistor. The key is closed at time $t=t_0$. Which of the following statement(s) is(are) correct?

[Given: $e^{-1}=0.36$ ]

A bar of mass $M=1.00 \mathrm{~kg}$ and length $L=0.20 \mathrm{~m}$ is lying on a horizontal frictionless surface. One end of the bar is pivoted at a point about which it is free to rotate. A small mass $m=0.10 \mathrm{~kg}$ is moving on the same horizontal surface with $5.00 \mathrm{~m} \mathrm{~s}^{-1}$ speed on a path perpendicular to the bar. It hits the bar at a distance $L / 2$ from the pivoted end and returns back on the same path with speed v. After this elastic collision, the bar rotates with an angular velocity $\omega$.

Which of the following statement is correct?

A container has a base of $50 \mathrm{~cm} \times 5 \mathrm{~cm}$ and height $50 \mathrm{~cm}$, as shown in the figure. It has two parallel electrically conducting walls each of area $50 \mathrm{~cm} \times 50 \mathrm{~cm}$. The remaining walls of the container are thin and non-conducting. The container is being filled with a liquid of dielectric constant 3 at a uniform rate of $250 \mathrm{~cm}^3 \mathrm{~s}^{-1}$. What is the value of the capacitance of the container after 10 seconds?

[Given: Permittivity of free space $\epsilon_0=9 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}$, the effects of the non-conducting walls on the capacitance are negligible]

One mole of an ideal gas expands adiabatically from an initial state $\left(T_{\mathrm{A}}, V_0\right)$ to final state $\left(T_{\mathrm{f}}, 5 V_0\right)$. Another mole of the same gas expands isothermally from a different initial state $\left(T_{\mathrm{B}}, V_0\right)$ to the same final state $\left(T_{\mathrm{f}}, 5 V_0\right)$. The ratio of the specific heats at constant pressure and constant volume of this ideal gas is $\gamma$. What is the ratio $T_{\mathrm{A}} / T_{\mathrm{B}}$ ?

Two satellites $\mathrm{P}$ and $\mathrm{Q}$ are moving in different circular orbits around the Earth (radius $R$ ). The heights of $\mathrm{P}$ and $\mathrm{Q}$ from the Earth surface are $h_{\mathrm{P}}$ and $h_{\mathrm{Q}}$, respectively, where $h_{\mathrm{P}}=R / 3$. The accelerations of $\mathrm{P}$ and $\mathrm{Q}$ due to Earth's gravity are $g_{\mathrm{P}}$ and $g_{\mathrm{Q}}$, respectively. If $g_{\mathrm{P}} / g_{\mathrm{Q}}=36 / 25$, what is the value of $h_{\mathrm{Q}}$ ?

A Hydrogen-like atom has atomic number $Z$. Photons emitted in the electronic transitions from level $n=4$ to level $n=3$ in these atoms are used to perform photoelectric effect experiment on a target metal. The maximum kinetic energy of the photoelectrons generated is $1.95 \mathrm{eV}$. If the photoelectric threshold wavelength for the target metal is $310 \mathrm{~nm}$, the value of $Z$ is _________.

[Given: $h c=1240 \mathrm{eV}-\mathrm{nm}$ and $R h c=13.6 \mathrm{eV}$, where $R$ is the Rydberg constant, $h$ is the Planck's constant and $c$ is the speed of light in vacuum]

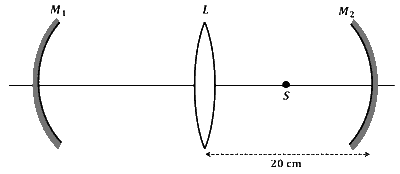
An optical arrangement consists of two concave mirrors $M_1$ and $M_2$, and a convex lens $L$ with a common principal axis, as shown in the figure. The focal length of $\mathrm{L}$ is $10 \mathrm{~cm}$. The radii of curvature of $M_1$ and $M_2$ are $20 \mathrm{~cm}$ and $24 \mathrm{~cm}$, respectively. The distance between $L$ and $M_2$ is $20 \mathrm{~cm}$. A point object $S$ is placed at the mid-point between $\mathrm{L}$ and $M_2$ on the axis. When the distance between $\mathrm{L}$ and $\mathrm{M}_1$ is $n / 7 \mathrm{~cm}$, one of the images coincides with $\mathrm{S}$. The value of $n$ is _______.

In an experiment for determination of the focal length of a thin convex lens, the distance of the object from the lens is $10 \pm 0.1 \mathrm{~cm}$ and the distance of its real image from the lens is $20 \pm 0.2 \mathrm{~cm}$. The error in the determination of focal length of the lens is $n \%$. The value of $n$ is ______.

A closed container contains a homogeneous mixture of two moles of an ideal monatomic gas $(\gamma=5 / 3)$ and one mole of an ideal diatomic gas $(\gamma=7 / 5)$. Here, $\gamma$ is the ratio of the specific heats at constant pressure and constant volume of an ideal gas. The gas mixture does a work of 66 Joule when heated at constant pressure. The change in its internal energy is _______ Joule.

A person of height $1.6 \mathrm{~m}$ is walking away from a lamp post of height $4 \mathrm{~m}$ along a straight path on the flat ground. The lamp post and the person are always perpendicular to the ground. If the speed of the person is $60 \mathrm{~cm} \mathrm{~s}^{-1}$, the speed of the tip of the person's shadow on the ground with respect to the person is ____________ $\mathrm{cm}~ \mathrm{s}^{-1}$.

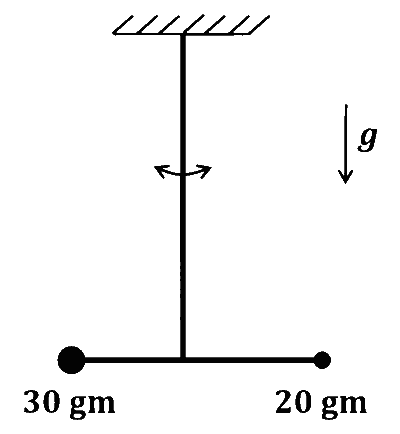
Two point-like objects of masses $20 ~\mathrm{gm}$ and $30 ~\mathrm{gm}$ are fixed at the two ends of a rigid massless rod of length $10 \mathrm{~cm}$. This system is suspended vertically from a rigid ceiling using a thin wire attached to its center of mass, as shown in the figure. The resulting torsional pendulum undergoes small oscillations. The torsional constant of the wire is $1.2 \times 10^{-8} \mathrm{~N} \mathrm{~m} ~\mathrm{rad}^{-1}$. The angular frequency of the oscillations in $n \times 10^{-3} ~\mathrm{rad} ~\mathrm{s}^{-1}$. The value of $n$ is _________ .

List-I shows different radioactive decay processes and List-II provides possible emitted particles. Match each entry in List-I with an appropriate entry from List-II, and choose the correct option.

List - I	List - II
(P) ${ }_{92}^{238} U \rightarrow{ }_{91}^{234} \mathrm{~Pa}$	(1) one $\alpha$ particle and one $\beta^{+}$particle
(Q) ${ }_{82}^{214} \mathrm{~Pb} \rightarrow{ }_{82}^{210} \mathrm{~Pb}$	(2) three $\beta^{-}$particles and one $\alpha$ particle
(R) ${ }_{81}^{210} \mathrm{Tl} \rightarrow{ }_{82}^{206} \mathrm{~Pb}$	(3) two $\beta^{-}$particles and one $\alpha$ particle
(S) ${ }_{91}^{228} \mathrm{~Pa} \rightarrow{ }_{88}^{224} \mathrm{Ra}$	(4) one $\alpha$ particle and one $\beta^{-}$particle
	(5) one $\alpha$ particle and two $\beta^{+}$particles

Match the temperature of a black body given in List-I with an appropriate statement in List-II, and choose the correct option.

[Given: Wien's constant as $2.9 \times 10^{-3} \mathrm{~m}-\mathrm{K}$ and $\frac{h c}{e}=1.24 \times 10^{-6} \mathrm{~V}-\mathrm{m}$ ]

List - I	List - II
(P) $2000 \mathrm{~K}$	(1) The radiation at peak wavelength can lead to emission of photoelectrons from a metal of work function $4 \mathrm{eV}$.
(Q) $3000 \mathrm{~K}$	(2) The radiation at peak wavelength is visible to human eye.
(R) $5000 \mathrm{~K}$	(3) The radiation at peak emission wavelength will result in the widest central maximum of a single slit diffraction.
(S) $10000 \mathrm{~K}$	(4) The power emitted per unit area is $1 / 16$ of that emitted by a blackbody at temperature $6000 \mathrm{~K}$.
	(5) The radiation at peak emission wavelength can be used to image human bones.

A series LCR circuit is connected to a $45 \sin (\omega t)$ Volt source. The resonant angular frequency of the circuit is $10^5 ~\mathrm{rad}~ \mathrm{s}^{-1}$ and current amplitude at resonance is $I_0$. When the angular frequency of the source is $\omega=8 \times 10^4 ~\mathrm{rad} ~\mathrm{s}^{-1}$, the current amplitude in the circuit is $0.05 I_0$. If $L=50 ~\mathrm{mH}$, match each entry in List-I with an appropriate value from List-II and choose the correct option.

List - I	List - II
(P) $I_0$ in $\mathrm{mA}$	(1) 44.4
(Q) The quality factor of the circuit	(2) 18
(R) The bandwidth of the circuit in $\mathrm{rad}~ \mathrm{s}^{-1}$	(3) 400
(S) The peak power dissipated at resonance in Watt	(4) 2250
	(5) 500

A thin conducting rod $M N$ of mass $20 ~\mathrm{gm}$, length $25 \mathrm{~cm}$ and resistance $10 ~\Omega$ is held on frictionless, long, perfectly conducting vertical rails as shown in the figure. There is a uniform magnetic field $B_0=4 \mathrm{~T}$ directed perpendicular to the plane of the rod-rail arrangement. The rod is released from rest at time $t=0$ and it moves down along the rails. Assume air drag is negligible. Match each quantity in List-I with an appropriate value from List-II, and choose the correct option.

[Given: The acceleration due to gravity $g=10 \mathrm{~m} \mathrm{~s}^{-2}$ and $e^{-1}=0.4$ ]

List - I	List - II
(P) At $t=0.2 \mathrm{~s}$, the magnitude of the induced emf in Volt	(1) 0.07
(Q) At $t=0.2 \mathrm{~s}$, the magnitude of the magnetic force in Newton	(2) 0.14
(R) At $t=0.2 \mathrm{~s}$, the power dissipated as heat in Watt	(3) 1.20
(S) The magnitude of terminal velocity of the rod in $\mathrm{m} \mathrm{s}^{-1}$	(4) 0.12
	(5) 2.00