JEE Advance - Physics (2023 - Paper 1 Online - No. 1)
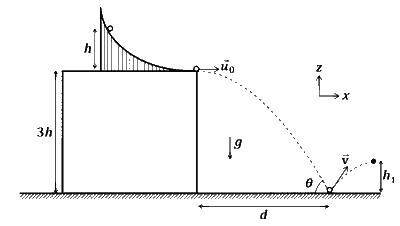
Explanation
Reflect on the scenario of a ball sliding down a frictionless slope. Initially at rest, the ball descends through a height h. Applying the principle of conservation of mechanical energy, we deduce that the initial speed $ u_0 $ is given by $ u_0 = \sqrt{2gh} $. Consequently, the velocity of the ball as it reaches the end of the slide can be expressed as :
$
\vec{u}_0 = \sqrt{2gh} \, \hat{\imath} .
$
In this scenario where a ball is launched horizontally with an initial speed $ u_0 $ from the top of a building that is $ 3h $ tall, we calculate the time $ t $ it takes for the ball to descend the vertical distance of $ 3h $. This time duration can be determined using the equation of motion under gravity, leading to :
$
t = \sqrt{\frac{2(3h)}{g}} = \sqrt{\frac{6h}{g}}.
$
Considering the horizontal distance covered over the time period t, we can express it as :
$
d = u_0 t = \sqrt{2gh} \cdot \sqrt{\frac{6h}{g}} = 2\sqrt{3}h
$ ..............(1)
When the ball impacts the ground, its velocity $\vec{u}$ comprises two components : a horizontal component $u_x$ along $\hat{\imath}$ and a vertical component $u_y$ along $\hat{\jmath}$. The horizontal velocity component remains unchanged throughout the motion and is given by $u_x = \sqrt{2gh}$. On the other hand, the vertical velocity component just before the ball hits the ground can be described as :
$
u_y = -\sqrt{2g(3h)} = -\sqrt{6gh}
$
Now, let's focus on the ball's impact with the ground. Since the ground can only exert an impulse in the vertical direction, the horizontal momentum of the ball remains unchanged. This means the horizontal component of the ball's velocity after collision (represented as $ v \cos \phi )$ is equal to its horizontal velocity component before the collision. Therefore, we can write this relationship as :
$
v \cos \phi = u_x = \sqrt{2gh}
$ ..........(2)
In the vertical axis, the approach velocity, denoted as $ v_a $, equals the absolute value of $ u_y $, which is $ \sqrt{6gh} $. The separation velocity, denoted as $ v_s $, is expressed as $ v \sin \phi $. Using the coefficient of restitution $ e $, which is defined as $ \frac{1}{\sqrt{3}} $, we can establish the relationship :
$
e = \frac{1}{\sqrt{3}} = \frac{v_s}{v_a} = \frac{v \sin \phi}{\sqrt{6gh}}.
$
This equation leads to the conclusion that :
$
v \sin \phi = \sqrt{2gh}
$ ...............(3)
From these two equations (2) and (3), it's clear that $ v \cos \phi $ and $ v \sin \phi $ are equal. This equality suggests that $ \phi = 45^\circ $, as the sine and cosine of 45 degrees are equal.
To find $ v $, we can use either of the two equations. Let's use the first one :
$ v \cos 45^\circ = \sqrt{2gh} $
Since $ \cos 45^\circ = \frac{1}{\sqrt{2}} $, we can rearrange and solve for $ v $:
$ v = \sqrt{2gh} \times \sqrt{2} = \sqrt{4gh} $
Thus, $ \phi = 45^\circ $ and $ v = \sqrt{4gh} $.
The ball bounces off with velocity $ \vec{v} $ composed of both horizontal and vertical components, as we have established that both $ v \cos \phi $ and $ v \sin \phi $) are equal to $ \sqrt{2gh} $, and the angle $ \phi $ is $ 45^\circ $.
In vector form, the velocity of the ball after bouncing can be represented as the sum of its horizontal and vertical components. Given that both components are equal to $ \sqrt{2gh} $ and considering the direction of these components along the unit vectors $ \hat{\imath} $ (horizontal) and $ \hat{\jmath} $ (vertical), the velocity vector $ \vec{v} $ can be expressed as :
$
\vec{v} = \sqrt{2gh}\hat{\imath} + \sqrt{2gh}\hat{\jmath}.
$
$$ \Rightarrow $$ $ \vec{v} = \sqrt{2gh}(\hat{\imath} + \hat{\jmath}). $
This equation indicates that after the collision, the ball bounces off with equal horizontal and vertical velocity components, each of magnitude $ \sqrt{2gh} $.
The peak height, $ h_1 $, achieved during the projectile's trajectory from point C to D, can be calculated using the formula :
$
h_1 = \frac{v^2 \sin^2 \phi}{2g}.
$
In this scenario, where $ v = \sqrt{4gh} $ and $ \phi = 45^\circ $, the expression becomes :
$
h_1 = \frac{(\sqrt{4gh})^2 \sin^2 45^\circ}{2g}.
$
Using the fact that $ \sin 45^\circ $ is $ \frac{1}{\sqrt{2}} $ and simplifying, we find that :
$
h_1 = h = \frac{d}{2\sqrt{3}},
$
where the equation (1) has been applied to establish the relationship.
Comments (0)


