JEE Advance - Physics (2023 - Paper 1 Online - No. 13)
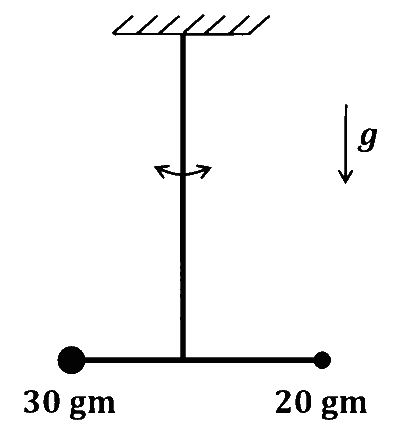
Two point-like objects of masses $20 ~\mathrm{gm}$ and $30 ~\mathrm{gm}$ are fixed at the two ends of a rigid massless rod of length $10 \mathrm{~cm}$. This system is suspended vertically from a rigid ceiling using a thin wire attached to its center of mass, as shown in the figure. The resulting torsional pendulum undergoes small oscillations. The torsional constant of the wire is $1.2 \times 10^{-8} \mathrm{~N} \mathrm{~m} ~\mathrm{rad}^{-1}$. The angular frequency of the oscillations in $n \times 10^{-3} ~\mathrm{rad} ~\mathrm{s}^{-1}$. The value of $n$ is _________ .

Answer
10
Explanation
$\begin{aligned} & m_1=30 \mathrm{gm} \\\\ & m_2=20 \mathrm{gm}\end{aligned}$

Moment of inertia about the axis of rotation is
$$ I=m_1 r_1^2+m_2 r_2^2 $$
Clearly $r_1=4 \mathrm{~cm}$
And $r_2=6 \mathrm{~cm}$
$$ \begin{aligned} & \therefore I=\left(30 \times 10^{-3} \times 16 \times 10^{-4}\right)+\left(20 \times 10^{-3} \times 36 \times 10^{-4}\right) \\\\ & \Rightarrow I=1200 \times 10^{-7} \mathrm{~kg} \mathrm{~m}^2 \end{aligned} $$
If the system is rotated by small angle ' $\theta$ ', the restoring torque is $\tau_{(R)}=-k \theta$
And $\frac{d^2 \theta}{d t^2}=\frac{-k}{l} \cdot \theta=-\omega^2 \theta=\frac{-1.2 \times 10^{-8}}{1200 \times 10^{-7}} \cdot \theta$
$$ \therefore \omega^2=10^{-4} $$
$\begin{aligned} & \text { So, } \omega=\frac{1}{100} \mathrm{rad} / \mathrm{s} \\\\ & \Rightarrow \omega=10 \times 10^{-3} \mathrm{rad} / \mathrm{s}\end{aligned}$

Moment of inertia about the axis of rotation is
$$ I=m_1 r_1^2+m_2 r_2^2 $$
Clearly $r_1=4 \mathrm{~cm}$
And $r_2=6 \mathrm{~cm}$
$$ \begin{aligned} & \therefore I=\left(30 \times 10^{-3} \times 16 \times 10^{-4}\right)+\left(20 \times 10^{-3} \times 36 \times 10^{-4}\right) \\\\ & \Rightarrow I=1200 \times 10^{-7} \mathrm{~kg} \mathrm{~m}^2 \end{aligned} $$
If the system is rotated by small angle ' $\theta$ ', the restoring torque is $\tau_{(R)}=-k \theta$
And $\frac{d^2 \theta}{d t^2}=\frac{-k}{l} \cdot \theta=-\omega^2 \theta=\frac{-1.2 \times 10^{-8}}{1200 \times 10^{-7}} \cdot \theta$
$$ \therefore \omega^2=10^{-4} $$
$\begin{aligned} & \text { So, } \omega=\frac{1}{100} \mathrm{rad} / \mathrm{s} \\\\ & \Rightarrow \omega=10 \times 10^{-3} \mathrm{rad} / \mathrm{s}\end{aligned}$
Comments (0)


