Sign In

JEE Advance - Physics (2023 - Paper 1 Online - No. 6)

One mole of an ideal gas expands adiabatically from an initial state $\left(T_{\mathrm{A}}, V_0\right)$ to final state $\left(T_{\mathrm{f}}, 5 V_0\right)$. Another mole of the same gas expands isothermally from a different initial state $\left(T_{\mathrm{B}}, V_0\right)$ to the same final state $\left(T_{\mathrm{f}}, 5 V_0\right)$. The ratio of the specific heats at constant pressure and constant volume of this ideal gas is $\gamma$. What is the ratio $T_{\mathrm{A}} / T_{\mathrm{B}}$ ?
$5^{\gamma-1}$
$5^{1-\gamma}$
$5^\gamma$
$5^{1+\gamma}$

Explanation

JEE Advanced 2023 Paper 1 Online Physics - Heat and Thermodynamics Question 9 English Explanation

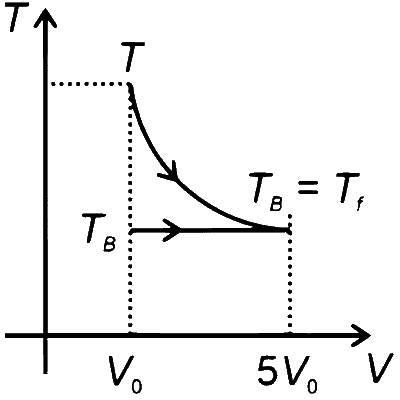
The expansion of an ideal gas can be analyzed using the thermodynamic relations for adiabatic and isothermal processes.

  1. Adiabatic Expansion: For an adiabatic process, we use the relation involving temperatures and volumes at the initial and final states, which is given by :

    $ TV^{\gamma-1} = \text{constant} $

    Therefore, for the adiabatic expansion from $(T_A, V_0)$ to $(T_f, 5V_0)$, we have :

    $ T_A V_0^{\gamma-1} = T_f (5V_0)^{\gamma-1} $

    Simplifying, we get : $ T_A = T_f \times 5^{\gamma-1} $

  2. Isothermal Expansion : In an isothermal process, the temperature remains constant. So, $ T_B = T_f $ for the isothermal expansion from $(T_B, V_0)$ to $(T_f, 5V_0)$.

To find the ratio $ T_A / T_B $, we substitute the expressions for $ T_A $ and $ T_B $ :

$ \frac{T_A}{T_B} = \frac{T_f \times 5^{\gamma-1}}{T_f} $

$ \frac{T_A}{T_B} = 5^{\gamma-1} $

Therefore, the ratio $ T_A / T_B $ is $ 5^{\gamma-1} $, which corresponds to Option A.

Comments (0)

Advertisement