JEE Advance - Physics (2023 - Paper 1 Online - No. 3)
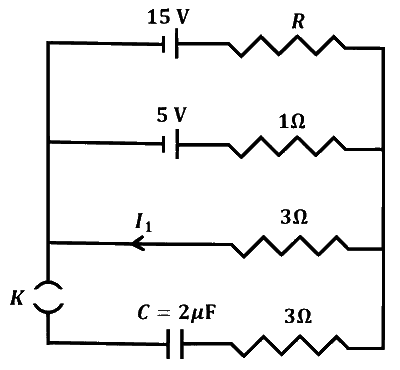
In a circuit shown in the figure, the capacitor $C$ is initially uncharged and the key $K$ is open. In this condition, a current of $1 \mathrm{~A}$ flows through the $1 \Omega$ resistor. The key is closed at time $t=t_0$. Which of the following statement(s) is(are) correct?
[Given: $e^{-1}=0.36$ ]
[Given: $e^{-1}=0.36$ ]

The value of the resistance $R$ is $3 \Omega$.
For $t < t_0 $, the value of current $I_1$ is $2 \mathrm{~A}$.
At $t=t_0+7.2 \mu \mathrm{s}$, the current in the capacitor is $0.6 \mathrm{~A}$.
For $t \rightarrow \infty$, the charge on the capacitor is $12 \mu \mathrm{C}$.
Explanation
At $\mathbf{t}<\mathbf{t}_0$,



At $\mathbf{t} < \mathbf{t}_0$
$$ \begin{aligned} i & =\frac{\left(\frac{45}{3+R}\right)-5}{1=\frac{3 R}{3+R}} \\\\ 1 & =\frac{45-15-5 R}{3+4 R} \\\\ \Rightarrow R & =3 \Omega \end{aligned} $$
(A) is correct.
$$ I_1=\frac{\frac{15}{2}}{3+\frac{3}{4}} \Rightarrow I_1=2 \mathrm{~A} $$
(B) is correct.
At $\mathbf{t} > \mathbf{t}_0$

$\begin{aligned} \frac{\varepsilon}{r} & =\frac{15}{3}+\frac{5}{1}+\frac{0}{3} \\\\ \frac{1}{r} & =\frac{1}{3}+\frac{1}{1}+\frac{1}{3}=\frac{5}{3} \\\\ \varepsilon & =10 \times \frac{3}{5} \Rightarrow 6 \mathrm{~V} \\\\ \text { At } t \rightarrow \infty & \\\\ q & =\mathrm{C} \varepsilon \\\\ & =2 \times 10^{-6} \times 6=12 \mu \mathrm{C}\end{aligned}$
$\begin{aligned} & \text { Time constant } \tau=R C \\\\ & =(r+3) 2 \mu \mathrm{C} \\\\ & =\left(\frac{3}{5}+3\right) \times 12=7.2 \mu \mathrm{s} \\\\ & i=i . e^{-t / \tau} \\\\ & i_0=\frac{\varepsilon}{r+3}=\frac{6}{\left(3+\frac{3}{5}\right)}\end{aligned}$
$$ \begin{aligned} \Rightarrow \quad i & =\frac{6}{\frac{18}{5}} \times e^{-7.2 / 1.2} \\\\ & =\frac{5}{3} \times 0.36=0.6 \mathrm{~A} \end{aligned} $$
All options are correct.



At $\mathbf{t} < \mathbf{t}_0$
$$ \begin{aligned} i & =\frac{\left(\frac{45}{3+R}\right)-5}{1=\frac{3 R}{3+R}} \\\\ 1 & =\frac{45-15-5 R}{3+4 R} \\\\ \Rightarrow R & =3 \Omega \end{aligned} $$
(A) is correct.
$$ I_1=\frac{\frac{15}{2}}{3+\frac{3}{4}} \Rightarrow I_1=2 \mathrm{~A} $$
(B) is correct.
At $\mathbf{t} > \mathbf{t}_0$

$\begin{aligned} \frac{\varepsilon}{r} & =\frac{15}{3}+\frac{5}{1}+\frac{0}{3} \\\\ \frac{1}{r} & =\frac{1}{3}+\frac{1}{1}+\frac{1}{3}=\frac{5}{3} \\\\ \varepsilon & =10 \times \frac{3}{5} \Rightarrow 6 \mathrm{~V} \\\\ \text { At } t \rightarrow \infty & \\\\ q & =\mathrm{C} \varepsilon \\\\ & =2 \times 10^{-6} \times 6=12 \mu \mathrm{C}\end{aligned}$
$\begin{aligned} & \text { Time constant } \tau=R C \\\\ & =(r+3) 2 \mu \mathrm{C} \\\\ & =\left(\frac{3}{5}+3\right) \times 12=7.2 \mu \mathrm{s} \\\\ & i=i . e^{-t / \tau} \\\\ & i_0=\frac{\varepsilon}{r+3}=\frac{6}{\left(3+\frac{3}{5}\right)}\end{aligned}$
$$ \begin{aligned} \Rightarrow \quad i & =\frac{6}{\frac{18}{5}} \times e^{-7.2 / 1.2} \\\\ & =\frac{5}{3} \times 0.36=0.6 \mathrm{~A} \end{aligned} $$
All options are correct.
Comments (0)


