JEE Advance - Physics (2023 - Paper 1 Online - No. 9)
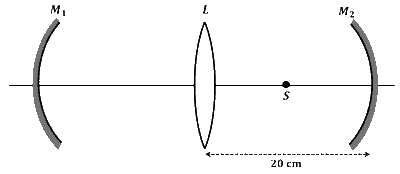
An optical arrangement consists of two concave mirrors $M_1$ and $M_2$, and a convex lens $L$ with a common principal axis, as shown in the figure. The focal length of $\mathrm{L}$ is $10 \mathrm{~cm}$. The radii of curvature of $M_1$ and $M_2$ are $20 \mathrm{~cm}$ and $24 \mathrm{~cm}$, respectively. The distance between $L$ and $M_2$ is $20 \mathrm{~cm}$. A point object $S$ is placed at the mid-point between $\mathrm{L}$ and $M_2$ on the axis. When the distance between $\mathrm{L}$ and $\mathrm{M}_1$ is $n / 7 \mathrm{~cm}$, one of the images coincides with $\mathrm{S}$. The value of $n$ is _______.

Answer
80
Explanation
Case-1 : if $\mathrm{I}^{\text {st }}$ refraction on lens :

$\mathrm{II}^{\text {nd }}$ refraction from $\mathrm{L}$ :-
$$ \begin{aligned} & \mathrm{u}=-(\mathrm{d}-10) \\\\ & \mathrm{f}=10 \mathrm{~cm} \\\\ & \frac{1}{\mathrm{v}}-\frac{1}{\mu}=\frac{1}{\mathrm{f}} \\\\ & \frac{1}{\mathrm{v}}+\frac{1}{\mathrm{~d}-10}=\frac{1}{10} \\\\ & \frac{1}{\mathrm{v}}=\frac{1}{10}-\frac{1}{(\mathrm{~d}-10)} .......(i) \end{aligned} $$
This $v$ will be object for $M_2$, and image should be at $10 \mathrm{~cm}$
$$ \begin{aligned} & \frac{1}{\mu}+\frac{1}{v_1}=\frac{1}{f} \\\\ & -\frac{1}{(20-v)}-\frac{1}{10}=-\frac{1}{12} \\\\ & \frac{1}{12}-\frac{1}{10}=\frac{1}{20-v} \\\\ & -\frac{2}{120}=\frac{1}{20-v} \\\\ & 20-v=-60 \\\\ & v=80 \mathrm{~cm} \end{aligned} $$
From equation (i), we get
$$ \begin{aligned} & \frac{1}{80}=\frac{1}{10}-\frac{1}{d-10} \\\\ & \frac{1}{d-10}=\frac{1}{10}-\frac{1}{80} \\\\ & \frac{1}{d-10}=\frac{80-10}{800}=\frac{70}{800} \\\\ & d-10=\frac{80}{7} \Rightarrow d=10+\frac{80}{7}=\frac{150}{7} \\\\ & n=150 \end{aligned} $$
Case-2 : If $1^{\text {st }}$ reflection on mirror $m_2$ :

For $\mathrm{m}_2$
$$ \begin{aligned} & \frac{1}{\mathrm{~V}_1}+\frac{1}{-10}=\frac{1}{-12} \\\\ & \mathrm{~V}_1=60 \mathrm{~cm} \end{aligned} $$
Then refraction on lens $\mathrm{L}$
$$ \begin{aligned} & \mathrm{u}_2=80 \mathrm{~cm} \\\\ & \frac{1}{\mathrm{~V}_2}-\frac{1}{-60}=\frac{1}{10} \\\\ & \mathrm{~V}_2=\frac{80}{7} \end{aligned} $$
Then reflection on $\mathrm{m}_2$
Either $V_2$ is at centre (normal incidence)
$$ \begin{aligned} & \mathrm{d}-\frac{80}{7}=20 \\\\ & \mathrm{~d}=\frac{220}{7} \\\\ & \frac{\mathrm{n}}{7}=\frac{220}{7} \\\\ & \mathrm{n}=220 \end{aligned} $$
$V_2$ is at pole of $m_2$
$$ \begin{aligned} & \mathrm{d}-\frac{80}{7}=0 \\\\ & \mathrm{~d}=\frac{80}{7} \\\\ & \frac{\mathrm{n}}{7}=\frac{80}{7} \\\\ & \mathrm{n}=80 \end{aligned} $$

Given that the object is positioned at the focal point, the resulting light rays will transition to a parallel alignment.
Upon the first reflection at Mirror $ M_1 $:
As the incoming light rays are parallel, the resultant image will be formed at the focal point.
$\mathrm{II}^{\text {nd }}$ refraction from $\mathrm{L}$ :-
$$ \begin{aligned} & \mathrm{u}=-(\mathrm{d}-10) \\\\ & \mathrm{f}=10 \mathrm{~cm} \\\\ & \frac{1}{\mathrm{v}}-\frac{1}{\mu}=\frac{1}{\mathrm{f}} \\\\ & \frac{1}{\mathrm{v}}+\frac{1}{\mathrm{~d}-10}=\frac{1}{10} \\\\ & \frac{1}{\mathrm{v}}=\frac{1}{10}-\frac{1}{(\mathrm{~d}-10)} .......(i) \end{aligned} $$
This $v$ will be object for $M_2$, and image should be at $10 \mathrm{~cm}$
$$ \begin{aligned} & \frac{1}{\mu}+\frac{1}{v_1}=\frac{1}{f} \\\\ & -\frac{1}{(20-v)}-\frac{1}{10}=-\frac{1}{12} \\\\ & \frac{1}{12}-\frac{1}{10}=\frac{1}{20-v} \\\\ & -\frac{2}{120}=\frac{1}{20-v} \\\\ & 20-v=-60 \\\\ & v=80 \mathrm{~cm} \end{aligned} $$
From equation (i), we get
$$ \begin{aligned} & \frac{1}{80}=\frac{1}{10}-\frac{1}{d-10} \\\\ & \frac{1}{d-10}=\frac{1}{10}-\frac{1}{80} \\\\ & \frac{1}{d-10}=\frac{80-10}{800}=\frac{70}{800} \\\\ & d-10=\frac{80}{7} \Rightarrow d=10+\frac{80}{7}=\frac{150}{7} \\\\ & n=150 \end{aligned} $$
Case-2 : If $1^{\text {st }}$ reflection on mirror $m_2$ :

For $\mathrm{m}_2$
$$ \begin{aligned} & \frac{1}{\mathrm{~V}_1}+\frac{1}{-10}=\frac{1}{-12} \\\\ & \mathrm{~V}_1=60 \mathrm{~cm} \end{aligned} $$
Then refraction on lens $\mathrm{L}$
$$ \begin{aligned} & \mathrm{u}_2=80 \mathrm{~cm} \\\\ & \frac{1}{\mathrm{~V}_2}-\frac{1}{-60}=\frac{1}{10} \\\\ & \mathrm{~V}_2=\frac{80}{7} \end{aligned} $$
Then reflection on $\mathrm{m}_2$
Either $V_2$ is at centre (normal incidence)
$$ \begin{aligned} & \mathrm{d}-\frac{80}{7}=20 \\\\ & \mathrm{~d}=\frac{220}{7} \\\\ & \frac{\mathrm{n}}{7}=\frac{220}{7} \\\\ & \mathrm{n}=220 \end{aligned} $$
$V_2$ is at pole of $m_2$
$$ \begin{aligned} & \mathrm{d}-\frac{80}{7}=0 \\\\ & \mathrm{~d}=\frac{80}{7} \\\\ & \frac{\mathrm{n}}{7}=\frac{80}{7} \\\\ & \mathrm{n}=80 \end{aligned} $$
Comments (0)


