JEE Advance - Physics (2023 - Paper 1 Online - No. 2)
A plane polarized blue light ray is incident on a prism such that there is no reflection from the surface of the prism. The angle of deviation of the emergent ray is $\delta=60^{\circ}$ (see Figure-1). The angle of minimum deviation for red light from the same prism is $\delta_{\min }=30^{\circ}$ (see Figure-2). The refractive index of the prism material for blue light is $\sqrt{3}$. Which of the following statement(s) is(are) correct?
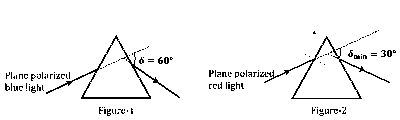

The blue light is polarized in the plane of incidence.
The angle of the prism is $45^{\circ}$.
The refractive index of the material of the prism for red light is $\sqrt{2}$.
The angle of refraction for blue light in air at the exit plane of the prism is $60^{\circ}$.
Explanation
When light strikes a surface at Brewster's angle, it becomes polarized perpendicular to the plane of incidence.
Therefore, there is no reflection of blue light observed.
This implies that the light must be polarized within the plane of incidence.

$\begin{aligned} \tan i & =\sqrt{3} \\\\ i & =60^{\circ} \\\\ \delta & =i+e-A \\\\ 60 & =60+e-A \\\\ \Rightarrow A & =e\end{aligned}$
$\begin{aligned} \frac{\sin i}{\sin r_1} & =\sqrt{3} \\\\ \Rightarrow \frac{\sin 60}{\sin r_1} & =\sqrt{3} \Rightarrow r_1=30^{\circ}\end{aligned}$
$\begin{array}{rlrl}r_2 =A-r_1 \\\\ r \sin \left(A-r_1\right) =\sin e \\\\ \Rightarrow \sqrt{3} \sin (A-30) =\sin A \\\\ r_3\left[\sin A \cos 30^{\circ}-\cos A\right. \sin 30]=\sin A \\\\ \Rightarrow \frac{\sqrt{3}}{2}(\sqrt{3}-\cot A) =1 \\\\ \Rightarrow \cot A =\sqrt{3}-\frac{2}{\sqrt{3}}=\frac{1}{\sqrt{3}} \\\\ \Rightarrow \cot A =\frac{1}{\sqrt{3}} \\\\ \Rightarrow A =60^{\circ}\end{array}$
So, $\quad e=60^{\circ}$ (for blue)
For red,
$$ \begin{aligned} \mu & =\frac{\sin \left(\frac{\delta_m+A}{2}\right)}{\sin \frac{A}{2}} \\\\ & =\frac{\sin \left(\frac{30+60}{2}\right)}{\sin \frac{60}{2}}=\frac{\sin 45}{\sin 30}=\frac{1 / \sqrt{2}}{1 / 2} \\\\ \mu_{\text {red }} & =\sqrt{2} \end{aligned} $$
(A), (C), (D) are correct.
Therefore, there is no reflection of blue light observed.
This implies that the light must be polarized within the plane of incidence.

$\begin{aligned} \tan i & =\sqrt{3} \\\\ i & =60^{\circ} \\\\ \delta & =i+e-A \\\\ 60 & =60+e-A \\\\ \Rightarrow A & =e\end{aligned}$
$\begin{aligned} \frac{\sin i}{\sin r_1} & =\sqrt{3} \\\\ \Rightarrow \frac{\sin 60}{\sin r_1} & =\sqrt{3} \Rightarrow r_1=30^{\circ}\end{aligned}$
$\begin{array}{rlrl}r_2 =A-r_1 \\\\ r \sin \left(A-r_1\right) =\sin e \\\\ \Rightarrow \sqrt{3} \sin (A-30) =\sin A \\\\ r_3\left[\sin A \cos 30^{\circ}-\cos A\right. \sin 30]=\sin A \\\\ \Rightarrow \frac{\sqrt{3}}{2}(\sqrt{3}-\cot A) =1 \\\\ \Rightarrow \cot A =\sqrt{3}-\frac{2}{\sqrt{3}}=\frac{1}{\sqrt{3}} \\\\ \Rightarrow \cot A =\frac{1}{\sqrt{3}} \\\\ \Rightarrow A =60^{\circ}\end{array}$
So, $\quad e=60^{\circ}$ (for blue)
For red,
$$ \begin{aligned} \mu & =\frac{\sin \left(\frac{\delta_m+A}{2}\right)}{\sin \frac{A}{2}} \\\\ & =\frac{\sin \left(\frac{30+60}{2}\right)}{\sin \frac{60}{2}}=\frac{\sin 45}{\sin 30}=\frac{1 / \sqrt{2}}{1 / 2} \\\\ \mu_{\text {red }} & =\sqrt{2} \end{aligned} $$
(A), (C), (D) are correct.
Comments (0)


