JEE Advance - Physics (2018 - Paper 1 Offline)
1
Two vectors $$\overrightarrow A $$ and $$\overrightarrow B $$ are defined as $$\overrightarrow A $$ $$=$$ $$a\widehat i$$ and $$\overrightarrow B = a$$ $$\left( {\cos \,\omega T\widehat i + \sin \,\omega t\,\widehat j} \right),$$ where $$a$$ is a constant and $$\omega = \pi /6\,\,rad{s^{ - 1}}.$$ If $$\left| {\overrightarrow A + \overrightarrow B } \right| = \sqrt 3 \left| {\overrightarrow A - \overrightarrow B } \right|$$ at time $$t = \tau $$ for the first time, the value of $$\tau ,$$ in second, is ______________.
Answer
2
2
Consider a body of mass $$1.0$$ $$kg$$ at rest at the origin at time $$t=0.$$ A force $$\overrightarrow F = \left( {\alpha t \widehat i + \beta \widehat j} \right)$$ is applied on the body, where $$\alpha = 1.0N{s^{ - 1}}$$ and $$\beta = 1.0\,N.$$ The torque acting on the body about the origin at time $$t=1.0s$$ is $$\overrightarrow \tau .$$ Which of the following statements is (are) true?
Answer
A
C
3
A uniform capillary tube of inner radius $$r$$ is dipped vertically into a beaker filled with water. The water rises to a height $$h$$ in the capillary tube above the water surface in the beaker. The surface tension of water is $$\sigma .$$ The angle of contact between water and the wall of the capillary tube is $$\theta .$$ Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
Answer
A
C
4
Two infinitely long straight wires lie in the $$xy$$-plane along the lines $$x = \pm R.$$ The wire located at $$x = + R$$ carries a constant current $${I_1}$$ and the wire located at $$x=-R$$ carries a constant current $${I_2}.$$ A circular loop of radius $$R$$ is suspended with its center at $$\left( {0,0,\sqrt 3 R} \right)$$ and in a plane parallel to the $$xy$$-plane. This loop carries a constant current $$I$$ in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the $$ + \widehat j$$ direction. which of the following statements regarding the magnetic field $$\overrightarrow B $$ is (are) true?
Answer
A
B
D
5
Two men are walking along a horizontal straight line in the same direction. The man in front walks at a speed $$1.0\,m{s^{ - 1}}$$ and the man behind walks at a speed $$2.0\,m{s^{ - 1}}.$$ A third man in standing at a height $$12$$ $$m$$ above the same horizontal line such that all three men are in a vertical plane. The two walking men are blowing identical whistles which emit a sound of frequency $$1430$$ $$Hz$$. The speed of sound in air is $$330\,m{s^{ - 1}}.$$ At the instant, when the moving men are $$10$$ $$m$$ apart, the stationary man is equidistant from them. The frequency of beats in $$Hz,$$ heard by the stationary man at this instant, is _____________.
Answer
5
6
A ring and disc are initially at rest, side by side, at the top of an inclined plane which makes an angle $${60^ \circ }$$ with the horizontal. They start to roll without slipping at the same instant of time along the shortest path. If the time difference between their reaching the ground is $$\left( {2 - \sqrt 3 } \right)/\sqrt {10} \,\,s,$$ then the height of the top of the inclined plane, in metres is ______________ . Take $$g = 10\,\,m{s^{ - 2}}.$$
Answer
0.75
7
A spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is $$2.0\,N{m^{ - 1}}$$ and the mass of the block is $$2.0$$ $$kg.$$ Ignore the mass of the spring. Initially the spring is an unstretched condition. Another block of mass $$1.0$$ $$kg$$ moving with a speed of $$2.0$$ $$m{s^{ - 1}}$$ collides elastically with the first block. The collision is such that the $$2.0$$ $$kg$$ block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is __________.
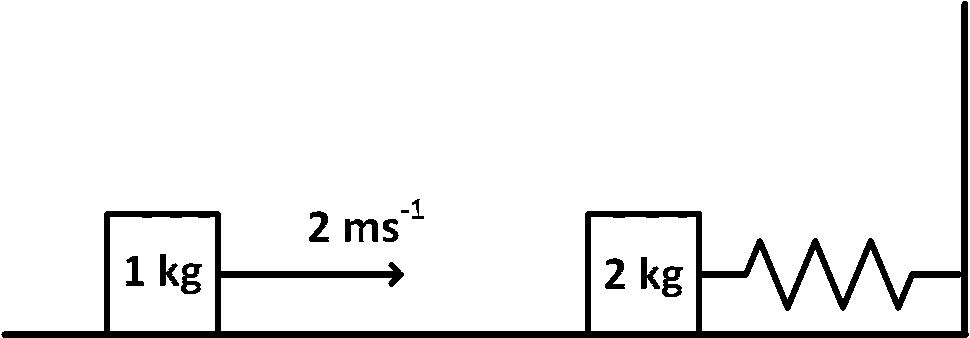

Answer
2.09
8
In the figure below, the switches $${S_1}$$ and $${S_2}$$ are closed simultaneously at $$t=0$$ and a current starts to flow in the circuit. Both the batteries have the same magnitude of the electromotive force (emf) and the polarities are as indicated in the figure. Ignore mutual inductance between the inductors. The current $$I$$ in the middle wire reaches its maximum magnitude $${I_{\max }}$$ at time $$t = \tau $$ . Which of the following statements is (are) true?


Answer
B
D
9
Three identical capacitors $${C_1},{C_2}$$ and $${C_3}$$ have a capacitance of $$1.0\,\mu F$$ each and they are unchanged initially. They are connected in a circuit as shown in the figure and $${C_1}$$ is then filled completely with a dielectric material of relative permittivity $${\varepsilon _r}.$$ The cell electromotive force $$\left( {emf} \right)\,\,{V_0} = 8V.$$ First the switch $${S_1}$$ is closed while the switch $${S_2}$$ is kept open. When the capacitor $${C_3}$$ is fully charged, $${S_1}$$ is opened and $${S_2}$$ is closed simultaneously. When all the capacitors reach equilibrium, the charge on $${C_3}$$ is found to be $$5\,\mu C.$$ The value of $${\varepsilon _r} = $$ _________________.
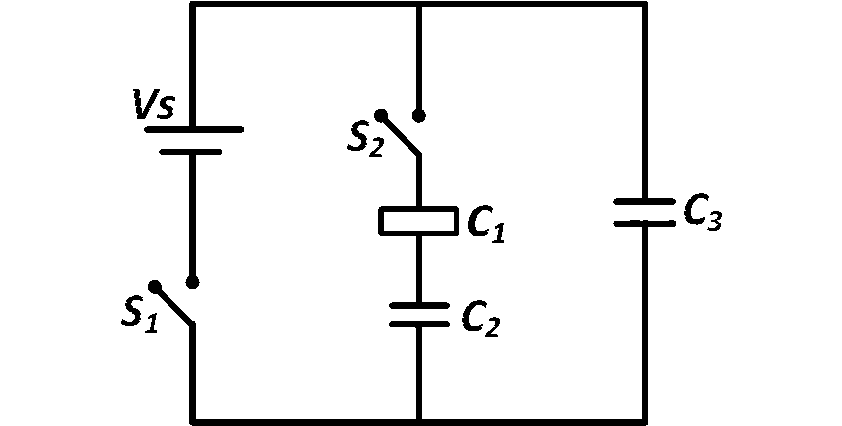

Answer
1.50
10
Consider a body of mass $$1.0$$ $$kg$$ at rest at the origin at time $$t=0.$$ A force $$\overrightarrow F = \left( {\alpha t \widehat i + \beta \widehat j} \right)$$ is applied on the body, where $$\alpha = 1.0N{s^{ - 1}}$$ and $$\beta = 1.0\,N.$$ The torque acting on the body about the origin at time $$t=1.0s$$ is $$\overrightarrow \tau .$$ Which of the following statements is (are) true?
Answer
A
C
11
A uniform capillary tube of inner radius $$r$$ is dipped vertically into a beaker filled with water. The water rises to a height $$h$$ in the capillary tube above the water surface in the beaker. The surface tension of water is $$\sigma .$$ The angle of contact between water and the wall of the capillary tube is $$\theta .$$ Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
Answer
A
C
12
Two infinitely long straight wires lie in the $$xy$$-plane along the lines $$x = \pm R.$$ The wire located at $$x = + R$$ carries a constant current $${I_1}$$ and the wire located at $$x=-R$$ carries a constant current $${I_2}.$$ A circular loop of radius $$R$$ is suspended with its center at $$\left( {0,0,\sqrt 3 R} \right)$$ and in a plane parallel to the $$xy$$-plane. This loop carries a constant current $$I$$ in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the $$ + \widehat j$$ direction. which of the following statements regarding the magnetic field $$\overrightarrow B $$ is (are) true?
Answer
A
B
D
13
In the $$xy$$-plane, the region $$y > 0$$ has a uniform magnetic field $${B_1}\widehat k$$ and the region $$y < 0$$ has another uniform magnetic field $${B_2}\widehat k.$$ A positively charged particle is projected from the origin along the positive $$y$$-axis with speed $${v_0} = \pi \,m{s^{ - 1}}$$ at $$t=0,$$ as shown in the figure. Neglect gravity in this problem. Let $$t=T$$ be the time when the particle crosses the $$x$$-axis from below for the first time. If $${B_2} = 4{B_1},$$ the average speed of the particle, in $$m{s^{ - 1}},$$ along the $$x$$-axis in the time interval $$T$$ is ___________.

Answer
2
14
In electromagnetic theory, the electric and magnetic phenomena are related to each other. Therefore, the dimensions of electric and magnetic quantities must also be related to each other. In the questions below, $$[E]$$ and $$[B]$$ stand for dimensions of electric and magnetic fields respectively, while $$\left[ {{\varepsilon _0}} \right]$$ and $$\left[ {{\mu _0}} \right]$$ stand for dimensions of the permittivity and permeability of free space respectively. $$\left[ L \right]$$ and $$\left[ T \right]$$ are dimensions of length and time respectively. All the quantities are given in $$SI$$ units.
The relation between $$\left[ {{\varepsilon _0}} \right]$$ and $$\left[ {{\mu _0}} \right]$$ is
The relation between $$\left[ {{\varepsilon _0}} \right]$$ and $$\left[ {{\mu _0}} \right]$$ is
Answer
(D)
$$\left[ {{\mu _0}} \right] = {\left[ {{\varepsilon _0}} \right]^{ - 1}}{\left[ L \right]^{ - 2}}{\left[ T \right]^2}$$
15
If the measurement errors in all the independent quantities are known, then it is possible to determine the error in any dependent quantity. This is done by the use of series expansion and truncating the expansion at the first power of the error. For example, consider the relation $$z = x/y.$$ If the errors in $$x,y$$ and $$z$$ are $$\Delta x,\Delta y$$ and $$\Delta z,$$ respectively, then
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
The series expansion for $${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}},$$ to first power in $$\Delta y/y.$$ is $$1 \pm \left( {\Delta y/y} \right).$$ The relative errors in independent variables are always added. So the error in $$z$$ will be
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
The above derivation makes the assumption that $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ Therefore, the higher powers of these quantities are neglected.
In an experiment the initial number of radioactive nuclei is $$3000.$$ It is found that $$1000 \pm 40$$ nuclei decayed in the first $$1.0s.$$ For $$\left| x \right| < < 1.$$ $$\ln \left( {1 + x} \right) = x$$ up to first power in $$x.$$ The error $$\Delta \lambda ,$$ in the determination of the decay constant $$\lambda ,$$ in $${s^{ - 1}},$$ is
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
The series expansion for $${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}},$$ to first power in $$\Delta y/y.$$ is $$1 \pm \left( {\Delta y/y} \right).$$ The relative errors in independent variables are always added. So the error in $$z$$ will be
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
The above derivation makes the assumption that $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ Therefore, the higher powers of these quantities are neglected.
In an experiment the initial number of radioactive nuclei is $$3000.$$ It is found that $$1000 \pm 40$$ nuclei decayed in the first $$1.0s.$$ For $$\left| x \right| < < 1.$$ $$\ln \left( {1 + x} \right) = x$$ up to first power in $$x.$$ The error $$\Delta \lambda ,$$ in the determination of the decay constant $$\lambda ,$$ in $${s^{ - 1}},$$ is
Answer
(C)
$$0.02$$
16
If the measurement errors in all the independent quantities are known, then it is possible to determine the error in any dependent quantity. This is done by the use of series expansion and truncating the expansion at the first power of the error. For example, consider the relation $$z = x/y.$$ If the errors in $$x,y$$ and $$z$$ are $$\Delta x,\Delta y$$ and $$\Delta z,$$ respectively, then
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
The series expansion for $${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}},$$ to first power in $$\Delta y/y.$$ is $$1 \pm \left( {\Delta y/y} \right).$$ The relative errors in independent variables are always added. So the error in $$z$$ will be
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
The above derivation makes the assumption that $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ Therefore, the higher powers of these quantities are neglected.
Consider the ratio $$r = {{\left( {1 - a} \right)} \over {1 + a}}$$ to be determined by measuring a dimensionless quantity $$a.$$ If the error in the measurement of $$a$$ is $$\Delta a\left( {\Delta a/a < < 1.} \right.$$ then what is the error $$\Delta r$$ in determining $$r$$?
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
The series expansion for $${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}},$$ to first power in $$\Delta y/y.$$ is $$1 \pm \left( {\Delta y/y} \right).$$ The relative errors in independent variables are always added. So the error in $$z$$ will be
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
The above derivation makes the assumption that $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ Therefore, the higher powers of these quantities are neglected.
Consider the ratio $$r = {{\left( {1 - a} \right)} \over {1 + a}}$$ to be determined by measuring a dimensionless quantity $$a.$$ If the error in the measurement of $$a$$ is $$\Delta a\left( {\Delta a/a < < 1.} \right.$$ then what is the error $$\Delta r$$ in determining $$r$$?
Answer
(B)
$${{2\Delta a} \over {{{\left( {1 + a} \right)}^2}}}$$
17
In electromagnetic theory, the electric and magnetic phenomena are related to each other. Therefore, the dimensions of electric and magnetic quantities must also be related to each other. In the questions below, $$[E]$$ and $$[B]$$ stand for dimensions of electric and magnetic fields respectively, while $$\left[ {{\varepsilon _0}} \right]$$ and $$\left[ {{\mu _0}} \right]$$ stand for dimensions of the permittivity and permeability of free space respectively. $$\left[ L \right]$$ and $$\left[ T \right]$$ are dimensions of length and time respectively. All the quantities are given in $$SI$$ units.
The relation between $$[E]$$ and $$[B]$$ is
The relation between $$[E]$$ and $$[B]$$ is
Answer
(C)
$$\left[ E \right] = \left[ B \right]\left[ L \right]{\left[ T \right]^{ - 1}}$$
18
The potential energy of a particle of mass $$m$$ at a distance $$r$$ from a fixed point $$O$$ is given by $$V\left( r \right) = k{r^2}/2,$$ where $$k$$ is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius $$R$$ about the point $$O$$. If $$v$$ is the speed of the particle and $$L$$ is the magnitude of its angular momentum about $$O,$$ which of the following statements is (are) true?
Answer
B
C

