The charged particle enters the magnetic field region at O. Its velocity is perpendicular to the field direction. The magnetic force on the particle, qv₀B₁, provides centripetal acceleration to move on a circular path from O to P. The radius of the circular path is given by

$${r_1} = m{v_0}/(q{B_1})$$.

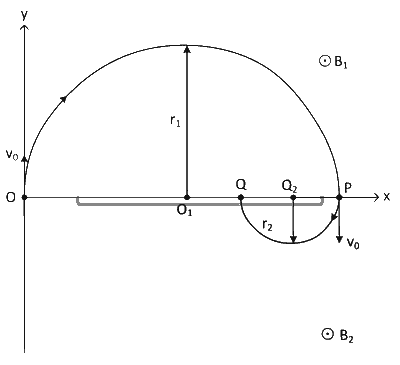
The time taken by the particle to travel from O to P is

$${T_1} = \pi {r_1}/{v_0} = \pi m/(q{B_1})$$

At P, the particle enters the magnetic field B₂ with its velocity perpendicular to the field direction. The magnetic force qv₀B₂ provides the centripetal acceleration to move in a circular path from P to Q. The radius of the circular path is

$${r_2} = m{v_0}/(q{B_2})$$.

The time taken by the particle to travel from P to Q is

$${T_2} = \pi {r_2}/{v_0} = \pi m/(q{B_2})$$.

AT Q, the particle crosses x-axis from below for the first time. Thus, T = T₁ + T₂. The average speed of the particle along the x-axis in the time interval T is given by

$$v = {{\int_0^T {{v_x}dt} } \over T} = {{\int_0^{{T_1}} {{v_{x1}}dt + \int_{{T_1}}^{{T_1} + {T_2}} {{v_{x2}}dt} } } \over {{T_1} + {T_2}}}$$

$$ = {{2{r_1} + 2{r_2}} \over {{T_1} + {T_2}}} = {{{{2m{v_0}} \over q}\left( {{1 \over {{B_1}}} + {1 \over {{B_2}}}} \right)} \over {{{\pi m} \over q}\left( {{1 \over {{B_1}}} + {1 \over {{B_2}}}} \right)}}$$

$$ = {{2{v_0}} \over \pi } = {{2(\pi )} \over \pi } = 2$$ m/s