Sign In

JEE Advance - Physics (2018 - Paper 1 Offline - No. 5)

Two men are walking along a horizontal straight line in the same direction. The man in front walks at a speed $$1.0\,m{s^{ - 1}}$$ and the man behind walks at a speed $$2.0\,m{s^{ - 1}}.$$ A third man in standing at a height $$12$$ $$m$$ above the same horizontal line such that all three men are in a vertical plane. The two walking men are blowing identical whistles which emit a sound of frequency $$1430$$ $$Hz$$. The speed of sound in air is $$330\,m{s^{ - 1}}.$$ At the instant, when the moving men are $$10$$ $$m$$ apart, the stationary man is equidistant from them. The frequency of beats in $$Hz,$$ heard by the stationary man at this instant, is _____________.
Answer
5

Explanation

From given data, we can draw the figure below.

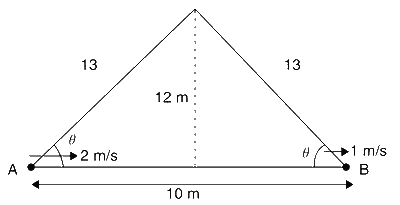
JEE Advanced 2018 Paper 1 Offline Physics - Waves Question 32 English Explanation

Now, frequency of man behind is

$${f_1} = f\left( {{v \over {v - {v_s}\cos \theta }}} \right)$$

where, x is speed of sound in air, vs is speed of man and f is frequency of whistle. Therefore,

$${f_1} = 1430\left( {{{330} \over {330 - 2 \times {5 \over {13}}}}} \right)$$

Frequency of man in front is

$${f_2} = f\left( {{v \over {v + {v_s}\cos \theta }}} \right) = 1430\left( {{{330} \over {330 + 1 \times {5 \over {13}}}}} \right)$$

Now, frequency of beat is given as

$$\Delta f = {f_1} - {f_2}$$

$$ = 1430\left( {{{330} \over {330 - {{10} \over {13}}}}} \right) - 1430\left( {{{330} \over {330 - {5 \over {13}}}}} \right)$$

$$ = 1430 \times 330\left( {\left[ {{1 \over {330 - {{10} \over {13}}}}} \right] - \left[ {{1 \over {330 - {5 \over {13}}}}} \right]} \right)$$

$$ = 1430 \times 330\left[ {{{13} \over {4280}} - {{13} \over {4295}}} \right]$$

$$ = {{1430 \times 330 \times 13 \times 15} \over {4280 \times 4295}}$$ = 5.0058 Hz $$\approx$$ 5.00 Hz

Comments (0)

Advertisement