JEE Advance - Physics (2018 - Paper 1 Offline - No. 7)
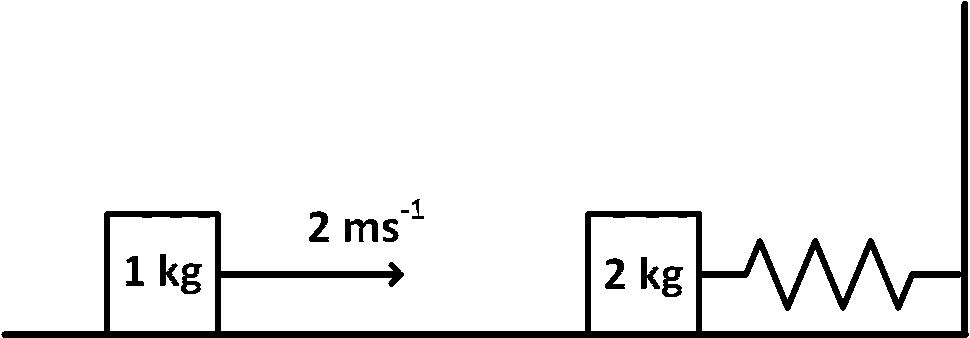
Explanation
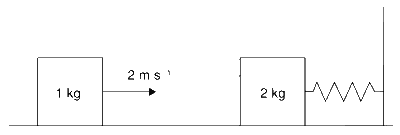
After collision the 2.0 kg block will perform simple harmonic oscillation with time period
$$T = 2\pi \sqrt {{m \over k}} $$
Given m = 2.0 kg and k = 2.0 N m$$-$$1, we have
T = 2$$\pi$$
Thus, the block returns to its original position in time
$$t = {T \over 2}$$ = $$\pi$$ s
That is, t = 3.14 s
Now, if v1 and v2 are velocities of 1.0 kg block and 2.0 kg block, respectively, before collision; v'1 and v'2 are velocities of 1.0 kg block and 2.0 block, respectively, after collision. So, by conservation of momentum
m1v1 + m2v2 = m1v'1 + m2v'2
Here, m1 = 1.0 kg, v1 is initial speed of 1.0 kg block = 2.0 m s$$-$$1, m2 = 2.0 kg, v2 is initial speed of 2.0 kg block = 0.0 m s$$-$$1, v'1 is final speed of 1.0 kg block after collision and v'2 is final speed of 2.0 kg block after collision. Then, 1.0 kg $$\times$$ 2.0 m/s + 2.0 kg $$\times$$ 0 m/s = 1.0 v'1 + 2.0 v'2
v'1 + 2v'2 = 2 ..... (1)
Also, using definition of coefficient of restitution
v'2 $$-$$ v'1 = $$\varepsilon $$(v1 $$-$$ v2)
Since collision is elastic, So $$\varepsilon $$ = 1
$$\Rightarrow$$ v'2 $$-$$ v'1 = v1 $$-$$ v2
$$\Rightarrow$$ v'2 $$-$$ v'1 = 2 $$-$$ 0
$$\Rightarrow$$ v'2 $$-$$ v'1 = 2 ...... (2)
From Eqs. (1) and (2), we get
$$v{'_2} = {4 \over 3}$$ m s$$-$$1 and $$v{'_1} = {-2 \over 3}$$ m s$$-$$1
Therefore, distance between the blocks is given as
$$s = v{'_1} \times t = {{ - 2} \over 3} \times 3.14 = 2.09$$ m
Comments (0)


