Sign In

JEE Advance - Physics (2018 - Paper 1 Offline - No. 1)

Two vectors $$\overrightarrow A $$ and $$\overrightarrow B $$ are defined as $$\overrightarrow A $$ $$=$$ $$a\widehat i$$ and $$\overrightarrow B = a$$ $$\left( {\cos \,\omega T\widehat i + \sin \,\omega t\,\widehat j} \right),$$ where $$a$$ is a constant and $$\omega = \pi /6\,\,rad{s^{ - 1}}.$$ If $$\left| {\overrightarrow A + \overrightarrow B } \right| = \sqrt 3 \left| {\overrightarrow A - \overrightarrow B } \right|$$ at time $$t = \tau $$ for the first time, the value of $$\tau ,$$ in second, is ______________.
Answer
2

Explanation

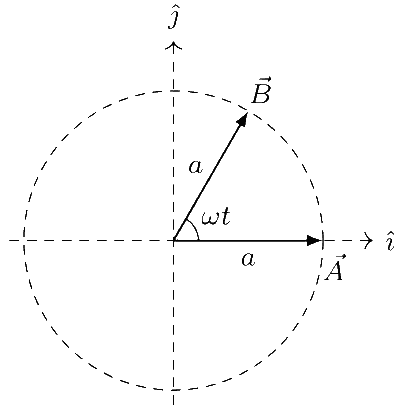
The vector $$\overrightarrow A = \alpha \widehat i$$ has a magnitude a and its direction is fixed. The vector $$\overrightarrow B = a(\cos \omega t\widehat i + \sin \omega t\widehat j)$$ rotates with an angular speed $$\omega$$ = $$\pi$$ / 6 rad/s in a circle of radius a. The magnitude of the sum and the difference of these vectors are given by

$$\left| {\overrightarrow A + \overrightarrow B } \right| = \left| {(a + a\cos \omega t)\widehat i + a\sin \omega t\widehat j} \right|$$

$$ = a\sqrt {{{(1 + \cos \omega t)}^2} + {{\sin }^2}\omega t} $$

$$ = 2a\cos (\omega t/2)$$.

$$\left| {\overrightarrow A - \overrightarrow B } \right| = \left| {(a - a\cos \omega t)\widehat i - a\sin \omega t\widehat j} \right|$$

$$ = 2a\sin (\omega t/2)$$

JEE Advanced 2018 Paper 1 Offline Physics - Rotational Motion Question 46 English Explanation

Hence,

$${{\left| {\overrightarrow A - \overrightarrow B } \right|} \over {\left| {\overrightarrow A + \overrightarrow B } \right|}} = \tan {{\omega t} \over 2} = {1 \over {\sqrt 3 }}$$,

which gives $$t = \tau = (2/\omega )(\pi /6) = 2$$ s.

Comments (0)

Advertisement