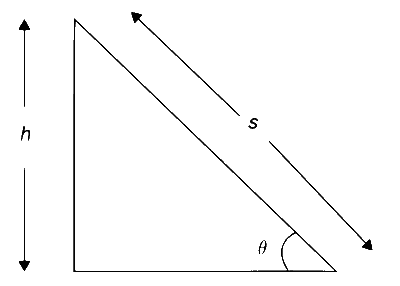
Given, h = height of the top of inclined plane = ?, $$\theta$$ = 60$$^\circ$$, g = 10 m s^$$-$$2 and time difference between ring and disc reaching ground = $${{2 - \sqrt 3 } \over {\sqrt {10} }}$$ s

We know that, $$a = {{g\sin \theta } \over {1 + {I \over {M{R^2}}}}}$$

For ring, $$I = M{R^2}$$ and for disc $$I = {3 \over 2}M{R^2}$$.

So, $${a_{ring}} = {{g\sin \theta } \over 2}$$ and $${a_{disk}} = {{2g\sin \theta } \over 3}$$

Now using $$s = {1 \over 2}a{t^2}$$

$${s_{ring}} = {1 \over 2}\left( {{{g\sin \theta } \over 2}} \right)t_1^2 \Rightarrow {h \over {\sin \theta }} = {1 \over 2}\left( {{{g\sin \theta } \over 2}} \right)t_1^2$$ ...... (1)

$${s_{disk}} = {1 \over 2}\left( {{{2g\sin \theta } \over 3}} \right)t_2^2 \Rightarrow {h \over {\sin \theta }} = {1 \over 2}\left( {{{2g\sin \theta } \over 3}} \right)t_2^2$$ ...... (2)

Given, $${t_1} - {t_2} = {{2 - \sqrt 3 } \over {\sqrt {10} }}$$

From Eq. (1), we have $${t_1} = \sqrt {{{4h} \over {g{{\sin }^2}\theta }}} $$

and from Eq. (2), we have $${t_2} = \sqrt {{{3h} \over {g{{\sin }^2}\theta }}} $$

So, $$\sqrt {{{4h} \over {g{{\sin }^2}\theta }}} - \sqrt {{{3h} \over {g{{\sin }^2}\theta }}} = {{2 - \sqrt 3 } \over {\sqrt {10} }}$$

$$ \Rightarrow \sqrt {{{4h} \over {10{{\sin }^2}60^\circ }}} - \sqrt {{{3h} \over {10{{\sin }^2}60^\circ }}} = {{2 - \sqrt 3 } \over {\sqrt {10} }}$$

$$ \Rightarrow \sqrt {{{16h} \over {3 \times 10}}} - \sqrt {{{4h} \over {10}}} = {{2 - \sqrt 3 } \over {\sqrt {10} }}$$

$$ \Rightarrow {{4\sqrt h } \over {\sqrt 3 }} - 2\sqrt h = 2 - \sqrt 3 $$

$$ \Rightarrow \sqrt h \left( {{4 \over {\sqrt 3 }} - 2} \right) = (2 - \sqrt 3 )$$

$$ \Rightarrow \sqrt h {{(4 - 2\sqrt 3 )} \over {\sqrt 3 }} = (2 - \sqrt 3 )$$

$$ \Rightarrow \sqrt h \times {2 \over {\sqrt 3 }}(2 - \sqrt 3 ) = (2 - \sqrt 3 ) \Rightarrow \sqrt h = {{\sqrt 3 } \over 2}$$

$$ \Rightarrow h = {3 \over 4} = 0.75$$ m