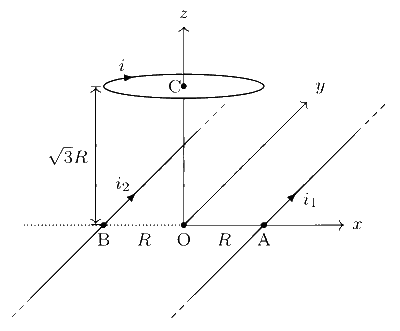
The magnetic field at the origin O (0, 0, 0) due to the infinitely long straight wire located at x = +R is

$${\overrightarrow B _1}(O) = {{{\mu _0}{i_1}} \over {2\pi R}}\widehat k$$

and due to the infinitely long straight wire located at x = $$-$$R is

$${\overrightarrow B _2}(O) = {{{\mu _0}{i_2}} \over {2\pi R}}( - \widehat k)$$.

The magnetic field at O due to the circular loop is

$${\overrightarrow B _3}(O) = {{{\mu _0}i{R^2}} \over {2{{({R^2} + {{(\sqrt 3 R)}^2})}^{3/2}}}}( - \widehat k) = {{{\mu _0}i} \over {16R}}( - \widehat k)$$.

The resultant magnetic field at the origin (0, 0, 0) is

$${\overrightarrow B _3}(O) = {\overrightarrow B _1}(O) + {\overrightarrow B _2}(O) + {\overrightarrow B _3}(O)$$

$$ = {{{\mu _0}} \over {16\pi R}}(8({i_1} - {i_2}) - \pi i)\widehat k$$.

Thus, if i₁ = i₂ then $${\overrightarrow B _1}(O) = - {\overrightarrow B _2}(O)$$ and $${\overrightarrow B _1}(O) = {\overrightarrow B _3}(O) \ne \overrightarrow 0 $$.

If i₁ > 0 and i₂ < 0 then both $${\overrightarrow B _1}(O)$$ and $${\overrightarrow B _2}(O)$$ are along $$\widehat k$$ but $${\overrightarrow B _3}(O)$$ is along $$-$$$$\widehat k$$. Thus, resultant field $$\overrightarrow B (O)$$ can be zero.

If i₁ < 0 and i₂ > 0 then $${\overrightarrow B _1}(O)$$, $${\overrightarrow B _2}(O)$$ and $${\overrightarrow B _3}(O)$$ are all along $$-$$$$\widehat k$$. Thus, resultant field $$\overrightarrow B (O)$$ cannot be zero. We encourage you to relate these results with the feasible solutions of 8(i₁ $$-$$ i₂) $$-$$ $$\pi$$i = 0 for i > 0.

Now, let us find the magnetic field at the centre of the loop i.e., point C in the figure.

The magnetic field $$\overrightarrow B_1$$ at the point C due to the infinitely long straight wire located x = +R is perpendicular to the line AC (see figure). It lies in the x-z plane and makes an angle 30$$^\circ$$ with the x axis. Resolve $$\overrightarrow B_1$$ along the x and z directions to get

$${{\vec B}_1}(C) = {{{\mu _0}{i_1}} \over {2\pi (2R)}}(\cos 30^\circ \widehat i + \sin 30^\circ \widehat k)$$.

Similarly, the magnetic field at C due to the infinitely long straight wire located at x = $$-$$R is

$${{\vec B}_2}(C) = {{{\mu _0}{i_2}} \over {2\pi (2R)}}(\cos 30^\circ \widehat i - \sin 30^\circ \widehat k)$$.

The magnetic field at C due to the circular loop is

$${{\vec B}_3}(C) = {{{\mu _0}i} \over {(2R)}}( - \widehat k)$$.

The resultant magnetic field at C is

$${{\vec B}_1}(C) = {{\vec B}_1}(C) + {{\vec B}_2}(C) + {{\vec B}_3}(C) = {{{\mu _0}} \over {8\pi R}}\left( {\sqrt 3 ({i_1} + {i_2})\widehat i + ({i_1} - {i_2} - 4\pi i)\widehat k} \right)$$.

If i₁ = i₂ then magnitudes of $${{\vec B}_1}(C)$$ and $${{\vec B}_2}(C)$$ are equal and their z-components are equal in magnitude but opposite in direction. Thus, z-component of the magnetic field at C is due to the circular loop only and its value is $$\left( { - {{{\mu _0}i} \over {2R}}} \right)$$.