कुछ पदार्थों में तापान्तर के कारण e.m.f. उत्पन्न हो सकता है। माना कि $S$ एक तार के सिरों के बीच उत्पन्न e.m.f. प्रति एकांक तापान्तर (e.m.f. per unit temperature difference) है| इस तार के पदार्थ की विद्युत् चालकता (electrical conductivity) और तापीय चालकता (thermal conductivity) क्रमशः $\sigma$ और $\kappa$ हैं। यदि $M, L, T, I$ और $K$ क्रमशः द्रव्यमान, लम्बाई, समय, धारा और तापमान की विमायें हों, तो $Z=\frac{S^2 \sigma}{\kappa}$ का विमीय सूत्र (dimensional formula) है:

दो समाक्षीय (co-axial) चालक बेलन चित्र 1 के अनुसार रखे हुए हैं। बेलनों की त्रिज्यायें $\sqrt{2} R$ एवं $2 R$ हैं और दोनों की लम्बाई $\ell$ है। आतंरिक बेलन पर आवेश $Q$ है और बाहरी बेलन को भूसंपर्कित (grounded) किया गया है। बेलनों के बीच के वलयाकार क्षेत्र (annular region) में $\kappa=5$ परावैद्युतांक (dielectric constant) का पदार्थ भरा है।। माना कि समान लम्बाई $\ell$ का एक काल्पनिक तल (imaginary plane) बेलनो के सम-अक्ष (common axis) से $R$ दूरी पर है| यह तल बेलनो की अक्ष के समांतर है| इस व्यवस्था के अनुप्रस्थ काट (cross-section) को चित्र 2 में दिखाया गया है। कोर-प्रभावों (edge effects) की उपेक्षा करते हुए, विद्युत् क्षेत्र का काल्पनिक तल से गुजरने वाला फ्लक्स (flux) है: ( $\epsilon_0$ मुक्त आकाश की विद्युतशीलता (permittivity) है)

एक $l$ लम्बाई की एकसमान छड़ $O O^{\prime}$ को बिन्दु $O$ पर चित्रानुसार हिंज (hinge) किया गया है। छड़ को दो समान कमानी स्थिरांक (spring constant) वाली द्रव्यमान रहित कमानियों (springs) की सहायता से दो दीवारों के बीच में ऊर्ध्वाधर रूप से रखा गया है| एक कमानी को छड़ के मध्य बिन्दु पर और दूसरी को सबसे ऊपरी बिन्दु $O^{\prime}$ पर चित्र 1 के अनुसार जोड़ा गया है। एक छोटे कोणीय विस्थापन (angular displacement) के कारण छड़ $f_1$ आवृत्ति के दोलन (oscillation) करती है। यदि दोनों कमानियों को छड़ के मध्य बिन्दु पर चित्र 2 के अनुसार जोड़ा जाता है तो एक छोटे कोणीय विस्थापन (angular displacement) के कारण छड़ $f_2$ आवृत्ति के दोलन (oscillation) करती है| गुरुत्वीय प्रभाव की उपेक्षा करते हुये और गति को आरेख (diagram) के तल में ही मानते हुये, $\frac{f_1}{f_2}$ का मान है:

माना कि $m_2 \mathrm{~kg}$ द्रव्यमान का एक तारा (star) $m_1 \mathrm{~kg}$ द्रव्यमान के दूसरे तारे के परितः वृत्ताकार कक्षा (circulas orbit) में परिक्रमा कर रहा है और $m_1 \gg m_2$ है। भारी तारा हल्के तारे से $\gamma \mathrm{kg} / \mathrm{s}$ की धीमी नियत दर (slow constant rate) से द्रव्यमान ग्रहण करता है। इस स्थानांतरण प्रक्रिया में द्रव्यमान की और कोई हानि नहीं होती है। यदि तारों के केंद्र बिन्दुओं के बीच की दूरी $r$ है तब इसकी सापेक्षिक परिवर्तन दर (relative rate of change) $\frac{1}{r} \frac{d r}{d t}\left(\mathrm{~s}^{-1}\right.$ में $)$ है:

एक $10^{-8} \mathrm{C}$ का धनात्मक बिंदु आवेश (positive point charge) एक 10 cm त्रिज्या (radius) वाले अनावेशित चालक गोले (neutral conducting sphere) के केंद्र से 20 cm की दूरी पर रखा है। इसके बाद गोले को भूसंपर्कित (grounded) किया जाता है, और गोले का आवेश मापा जाता है। फिर गोले का भूसंपर्क हटा दिया जाता है और तत्पश्चात बिंदु आवेश को गोले के केंद्र से त्रिज्य दिशा में 10 cm और दूर किया जाता है। $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2$ ( $\epsilon_0$ मुक्त आकाश की विद्युतशीलता (permittivity) है) लेते हुए निम्नलिखित कथनों में से कौन सा/से सही है/हैं:

दो समान फोकस दूरी (focal length) $f$ वाले समरूप (identical) अवतल दर्पण (concave mirror) आमनेसामने व्यवस्था आरेख (schematic diagram) के अनुसार रखे हुए हैं। फोकस दूरी $f$, दर्पणों के साइज़ से बहुत ज्यादा है। एक काँच की सिल्ली (glass slab) जिसकी मोटाई (thickness) $t$ और अपवर्तनांक (refractive index) $n_0$ है, दोनों दर्पणों से बराबर दूरी पर दर्पणों के सम मुख्य अक्ष (common principal axis) के लम्बवत रखी गयी है| एक एकवर्णी बिंदु प्रकाश स्रोत (monochromatic point light source) $S$, मुख्य अक्ष पर स्थित सिल्ली के मध्य बिंदु पर व्यवस्था आरेख के अनुसार अंतःस्थापित (embedded) है। प्रतिबिम्ब को $s$ पर ही बनने के लिए दोनों दर्पणों के बीच की निम्न दूरियों में से कौन सी/से दूरी(यां) सही है/हैं

एक समान दूरी पर रखी हुई छः अपरिमित कुचालक पतली परतें (infinitely large, non-conducting, thin sheets) विन्यासों (configurations) I और II के अनुसार स्थिर रखी हैं। परतों पर एकसमान पृष्ठ आवेश घनत्व (uniform surface charge densities) हैं, जिनको $\sigma_0$ के रूप में चित्रानुसार इंगित (indicated) किया गया है। कोई भी दो क्रमानुगत परतों के बीच की दूरी $1 \mu \mathrm{~m}$ है। परतों के बीच के विभिन्न भागों (regions) को $1,2,3,4$ और 5 से दर्शाया गया है। यदि $\sigma_0=9 \mu \mathrm{C} / \mathrm{m}^2$ है, तो निम्नलिखित कथनों में से कौन सा/से सही है/हैं: (मुक्त आकाश की विद्युतशीलता (permittivity of free space) का मान $\epsilon_0=9 \times 10^{-12} \mathrm{~F} / \mathrm{m}$ लें)

एक कार्नो इंजन, तापमान 1000 K पर स्थित एक गर्म ऊष्मा भंडार, (hot reservoir) के साथ कार्य कर रहा है| कार्नो इंजन की दक्षता (efficiency) 0.4 है| यह इंजन गर्म ऊष्मा भंडार से 150 J ऊष्मा एक चक्र में लेता है। इस इंजन से प्राप्त कार्य को एक उष्मा पंप को चलाने के लिए पूर्ण रूप से उपयोग किया जाता है। उष्मा पंप का निष्पादन गुणांक (coefficient of performance) 10 है| ऊष्मा पंप के गर्म ऊष्मा भंडार का तापमान 300 K है| निम्नलिखित कथनों में से कौन सा/से सही है/हैं

एक $M$ द्रव्यमान और $R$ त्रिज्या वाले ठोस चालक गोले पर $Q$ आवेश है| गोला अपने केंद्र से जाने वाली एक अक्ष के परितः एकसमान कोणीय चाल (uniform angular speed) $\omega$ से घूर्णन कर रहा है। उसी अक्ष के परितः चुम्बकीय द्विध्रुव आघूर्ण (magnetic dipole moment) और कोणीय संवेग (angular momentum) के परिमाणों का अनुपात $\alpha \frac{Q}{2 M}$ है | $\alpha$ का मान है ________

एक हाइड्रोजन परमाणु, जोकि आरम्भ में विरामावस्था में है, अपनी मूल अवस्था (ground state) में $v_1$ आवृत्ति के फोटोन को अवशोषित करता है और इससे 10 eV गतिज उर्जा का इलेक्ट्रॉन निकलता है| इस इलेक्ट्रॉन के विरामावस्था में स्थित एक पोजिट्रॉन (positron) के साथ मिलने से मूल अवस्था में स्थित एक पोजिट्रॉनियम परमाणु (positronium atom) बनता है जो उसी समय $v_2$ आवृत्ति का फोटोन उत्सर्जित करता है। परिणामस्वरुप बनने वाले पोजिट्रॉनियम परमाणु का द्रव्यमान केंद्र (center of mass) 5 eV की गतिज उर्जा के साथ गतिमान होता है। ये दिया गया है कि पोजिट्रॉन और इलेक्ट्रॉन का द्रव्यमान समान है और पोजिट्रॉनियम परमाणु को बोर परमाणु (Bohr atom) जैसा माना जा सकता है जहाँ पोजिट्रॉन और इलेक्ट्रॉन अपने द्रव्यमान केंद्र के परितः कक्षा में परिक्रमा करते हैं| माना कि इस पूरी प्रक्रिया में और कोई उर्जा क्षय (energy loss) नहीं होता है तो दोनों फोटोन की उर्जाओं में अंतर (eV में) है _________

एक आदर्श एकपरमाणुक (monatomic) गैस के $n$ मोल क्रमागत रूप से रुद्धोष्म (adiabatic) और समदाबी (isobaric) स्थैतिककल्प प्रक्रमों (quasi-static processes) से बने हुये WXYZW चक्र से गुजरते हैं, जैसा कि $V-T$ व्यवस्था आरेख (schematic diagram) में दिखाया गया है। गैस के आयतन $W, X$ एवं $Y$ बिन्दुओं पर क्रमशः $64 \mathrm{~cm}^3, 125 \mathrm{~cm}^3$ और $250 \mathrm{~cm}^3$ हैं। यदि बिंदु $W$ पर गैस का परम तापमान $T_W$ इस प्रकार है कि $n R T_W=1 \mathrm{~J}$ ( $R$ सार्वत्रिक गैस स्थिरांक (universal gas constant) है), तब गैस द्वारा $X Y$ पथ में अवशोषित ऊष्मा ( J में) है _________

एक भू-स्थिर (geostationary) उपग्रह विषुवत वृत्त (equator) के ऊपर पृथ्वी के परितः पृथ्वी के केंद्र से $r_1$ की नियत दूरी (fixed distance) पर एक कक्षा में परिक्रमण (orbiting) कर रहा है। एक दूसरा उपग्रह विषुवत वृत्त के तल (equatorial plane) में पृथ्वी के केंद्र से $r_2$ दूरी पर पृथ्वी के घूर्णन (rotation) की दिशा के विपरीत दिशा में परिक्रमण कर रहा है, जहाँ $r_1=1.21 r_2$ है। दूसरे उपग्रह का भू-स्थिर उपग्रह के सापेक्ष मापा गया आवर्तकाल (time period) $\frac{24}{p}$ घंटे (hours) है। $p$ का मान है _______

$L$ लम्बाई वाले एक ऊष्मीय रूप से विलगित पात्र (thermally isolated container) को क्षेत्रफल $A$ के एक ऊष्मीय चालक, चल (thermally conducting, movable) पिस्टन द्वारा बायें और दायें कोष्ठों (compartments) में विभाजित किया गया है। पात्र के बायें और दायें कोष्ठों में एक आदर्श गैस के क्रमशः $\frac{3}{2}$ और 1 मोल को रखा गया है। बायीं ओर के कोष्ठ में $k$ कमानी स्थिरांक (spring constant) और $\frac{2 L}{5}$ मूल लम्बाई (natural length) की एक कमानी (spring) को पिस्टन से संलग्र किया गया है। चित्रानुसार ऊष्मागतिक साम्य (thermodynamic equilibrium) में पिस्टन की पात्र के दोनों छोरों से दूरी $\frac{\mathrm{L}}{2}$ है। इस परिस्थिति में, यदि दायें कोष्ठ में दाब $P=\frac{\mathrm{kL}}{\mathrm{A}} \alpha$ है, तो $\alpha$ का मान है _________

यंग के एक द्विझिरी (double slit) प्रयोग में, कांच के दो वेज (wedges) $A$ और $B$, जिनके अपवर्तनांक (refractive index) के मान क्रमशः 1.7 और 1.5 हैं, का एक संयोजन झिरीयों के सामने चित्रानुसार रखा गया है। झिरीयों के बीच की दूरी $d=2 \mathrm{~mm}$ है। झिरीयों और परदे के बीच की निम्नतम दूरी $D=2 \mathrm{~m}$ है और वेज के संयोजन की मोटाई $t=12 \mu \mathrm{~m}$ है। चित्रानुसार $l$ का मान 1 mm है। दोनों वेज के तिरछे अन्तरापृष्ठ (slanted interface) पर अपवर्तन की उपेक्षा करें। कांच के वेज के संयोजन के कारण केंद्रीय उच्चिष्ठ (central maximum) का 0 के सापेक्ष विस्थापन (mm में) है _________

एक 200 g के प्रक्षेप्य (projectile) को क्षैतिज (horizontal) से $60^{\circ}$ के कोण पर $270 \mathrm{~m} / \mathrm{s}$ के प्रारंभिक वेग से श्यान माध्यम (viscous medium) में प्रक्षेपित किया जाता है| श्यान माध्यम में प्रक्षेप्य पर $\vec{F}=-c \vec{v}$ कर्षणबल (drag force) लगता है, जहाँ $c=0.1 \mathrm{~kg} / \mathrm{s}$ कर्ष गुणांक (drag coefficient) है और $\vec{v}$ प्रक्षेप्य का तात्क्षणिक वेग (instantaneous velocity) है| प्रक्षेप्य 2 s के पश्चात् एक ऊर्ध्वाधर दीवार से टकराता है। $e=2.7$ लेने पर दीवार की प्रक्षेपण बिंदु (point of projection) से क्षैतिज दूरी (m में) है ________

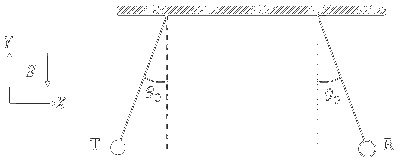
एक श्रव्य प्रेषित्र (audio transmitter) (T) और एक अभिग्राही (receiver) (R) दो समरूप (identical) द्रव्यमान रहित 8 m लम्बाई के धागों के द्वारा अपने कीलकों (pivots) से उर्ध्वाधर रूप में लटके हैं। दोनों कीलक $X$ अक्ष के अनुदिश एक दूसरे से बहुत दूर स्थित हैं। प्रेषित्र और अभिग्राही को उनकी साम्यावस्था से विपरीत दिशाओं में $X$ अक्ष के अनुदिश लघु कोणीय आयाम (small angular amplitude) $\theta_0=\cos ^{-1}(0.9)$ से खींच कर एक साथ छोड़ा जाता है| गुरुत्वीय त्वरण का मान $g=10 \mathrm{~m} / \mathrm{s}^2$ लें| यदि प्रेषित्र की प्राकृतिक आवृत्ति (natural frequency) 660 Hz है और वायु में ध्वनी की चाल $330 \mathrm{~m} / \mathrm{s}$ है, तब अभिग्राही द्वारा मापी गयी आवृत्ति में अधिकतम बदलाव ( Hz में) है ________