JEE Advance - Physics Hindi (2025 - Paper 2 Online - No. 16)
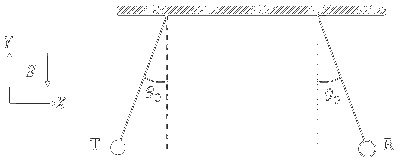
एक श्रव्य प्रेषित्र (audio transmitter) (T) और एक अभिग्राही (receiver) (R) दो समरूप (identical) द्रव्यमान रहित 8 m लम्बाई के धागों के द्वारा अपने कीलकों (pivots) से उर्ध्वाधर रूप में लटके हैं। दोनों कीलक $X$ अक्ष के अनुदिश एक दूसरे से बहुत दूर स्थित हैं। प्रेषित्र और अभिग्राही को उनकी साम्यावस्था से विपरीत दिशाओं में $X$ अक्ष के अनुदिश लघु कोणीय आयाम (small angular amplitude) $\theta_0=\cos ^{-1}(0.9)$ से खींच कर एक साथ छोड़ा जाता है| गुरुत्वीय त्वरण का मान $g=10 \mathrm{~m} / \mathrm{s}^2$ लें| यदि प्रेषित्र की प्राकृतिक आवृत्ति (natural frequency) 660 Hz है और वायु में ध्वनी की चाल $330 \mathrm{~m} / \mathrm{s}$ है, तब अभिग्राही द्वारा मापी गयी आवृत्ति में अधिकतम बदलाव ( Hz में) है ________
Explanation
$\begin{aligned} & \cos \theta_0=1-\frac{\theta_0^2}{2}=0.9 \\ & \frac{\theta_0^2}{2}=0.1 \Rightarrow \theta_0=10.2=\frac{1}{\sqrt{5}}\end{aligned}$

$$ \begin{aligned} & f_{\max }=\frac{v+v^{\prime}}{v-v^{\prime}} f \\ & f_{\min }=\frac{v-v^{\prime}}{v+v^{\prime}} f \\ & \Delta f_{\max }=f_{\max }-f_{\min }=\frac{v+v^{\prime}}{v-v^{\prime}} f-\frac{v-v^{\prime}}{v+v^{\prime}} f \\ & =\frac{\left(v+v^{\prime}\right)^2-\left(v-v^{\prime}\right)^2}{v^2-v^{\prime 2}} f \\ & \Delta f_{\max }=\frac{4 v v^{\prime}}{v^2-v^{\prime 2}} f ..........(i) \end{aligned} $$
यहाँ, $\mathrm{v}^{\prime}=\ell \Omega_{\max }$
$$ \begin{aligned} & =\ell \cdot \theta_0 \cdot \omega \quad(\omega=\text { कोणीय आवृत्ति }) \\ & =\ell \theta_0 \sqrt{\frac{\mathrm{~g}}{\ell}} \\ & \mathrm{v}^{\prime}=\theta_0 \sqrt{\mathrm{~g} \ell} \\ & \mathrm{v}^{\prime}=\frac{1}{\sqrt{5}} \sqrt{10 \times 8} \\ & \mathrm{v}^{\prime}=4 \end{aligned} $$
समीकरण (i) में रखें
$$ \begin{aligned} & \Delta f_{\max }=\frac{4 \times 330 \times 4 \times 660}{330^2-4^2} \\ & \approx \frac{16 \times 330 \times 660}{330} \approx 32 \end{aligned} $$
Comments (0)


