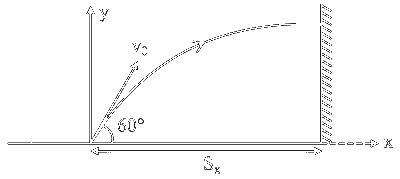
$$ \vec{F}_{\text{net}}=m \frac{d \vec{v}}{d t} $$

$$ m \overrightarrow{g}+\overrightarrow{F}=\frac{m d \overrightarrow{v}}{dt} $$

$$ m \overrightarrow{g}-C \overrightarrow{v}=\frac{m d \overrightarrow{v}}{dt} $$

क्षैतिज दिशा

$$ -C v_{x}=\frac{m d v_{x}}{dt} $$

$\begin{aligned} & -\frac{C}{m} \int_0^t d t=\int_{v_{0 x}}^{v_x} \frac{d v_x}{v_x} \\ & -\frac{t}{2}=\ln \frac{v_x}{v_{0 x}} \\ & \frac{d x}{d t}=v_x=v_{0 x} e^{-t / 2} \\ & \int_0^{s_x} d x=v_{0 x} \int_0^t e^{-t / 2} d t \\ & S_x=2 v_{0 x}\left(1-e^{-t / 2}\right)\end{aligned}$

t = 2 सेकंड पर

$\begin{aligned} & S_x=2 \times 270 \times \cos 60^{\circ}\left[1-\frac{1}{e}\right] \\ & S_x=270\left(1-\frac{1}{2.7}\right) \\ & =\frac{270}{2.7} \times(1.7) \\ & =170 \mathrm{~m} \\ & S_x=170 \mathrm{~m}\end{aligned}$