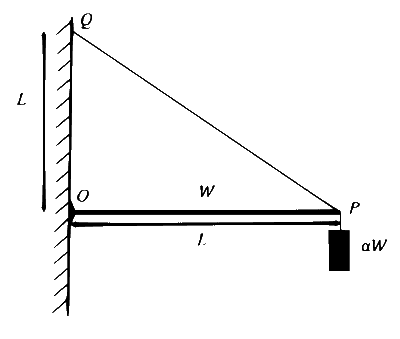
भार $$W$$ तथा लम्बाई $$L$$ की एक क्षैतिज (horizontal) एकसमान बीम (uniform beam) के एक सिरे को उर्ध्वाधर दीवार के एक बिन्दु $$O$$ पर कीलकित (hinged) किया गया है। बीम का दूसरा सिरा $$P$$ एक भारहीन अतान्य (inextensible) डोरी से बंधा है। डोरी का दूसरा सिरा $$Q$$, बिन्दु $$O$$ से $$L$$ ऊंचाई पर बंधा है। बीम के सिरे $$P$$ से $$\alpha W$$ भार का एक गुटका जुड़ा है, जैसा चित्र में दर्शाया गया है। चित्र पैमाने (scale) के अनुसार नहीं है| डोरी अधिकतम तनाव $$(2 \sqrt{2}) \mathrm{W}$$ वहन कर सकती है। निम्न में से कौन सा (से) कथन सही है (हैं) ?

एक ध्वनि स्रोत (source) गति $$u$$ से लम्बाई $$L$$ के एक स्थिर पाइप (pipe) के खुले छोर की ओर गतिमान है, और आवृत्ति (frequency) $$f_{s}$$ का ध्वनि उत्सर्जित कर रहा है। पाइप का दूसरा छोर बंद है। वायु में ध्वनि की गति $$v$$ है तथा पाइप की मूल आवृत्ति (fundamental frequency) $$f_{0}$$ है। निम्न में से $$u$$ तथा $$f_{s}$$ के किन संयोजन (नों) (combination(s)) के लिये, पाइप पर पहुँचने वाली ध्वनि अनुनाद (resonance) करेगी?

नीचे दिये गए चित्र में, प्रिज्म का प्रिज्म कोण $$\theta=60^{\circ}$$ है। प्रिज्म के बाएँ ओर के आधे हिस्से का अपवर्तनांक (refractive index) $$n_{1}$$ है और दाएँ और के आधे हिस्से का अपवर्तनांक $$n_{2}\left(n_{2} \geq n_{1}\right)$$ है। जब $$n_{1}=n_{2}=n=1.5$$ है तब आपतन कोण (angle of incidence) $$i$$ को इस तरह से लिया जाता है कि आपतित प्रकाश की किरणों का विचलन (deviation) न्यूनतम है। भित्र अपवर्तनांक, $$n_{1}=n$$ और $$n_{2}=n+\Delta n$$ (जहाँ $$\Delta n \ll n$$ ) की स्थिति में निर्गत कोण (angle of emergence) $$e=i+\Delta e$$ हो जाता है। निम्न कथनों में से कौन सा (से) सही है (हैं) ?

एक भौतिक राशि $$\vec{S}$$ को $$\vec{S}=(\vec{E} \times \vec{B}) / \mu_{0}$$ से परिभाषित किया जाता है, जहाँ $$\vec{E}$$ विद्युत क्षेत्र (electric field), $$\vec{B}$$ चुम्बकीय क्षेत्र (magnetic field) और $$\mu_{0}$$ निर्वात की चुंबकशीलता (permeability of free space) हैं। निम्न में से किसकी (किनकी) विमाएं $$\vec{S}$$ की विमाओं के समान हैं?

एक स्थिर भारी नाभिक (nucleus) $$N$$ का विखंडन (fission) $$N \rightarrow P+Q$$ समीकरण के अनुसार होता है, जहाँ $$P$$ और $$Q$$ दो हल्के नाभिक हैं। मान लीजिए कि $$\delta=M_{N}-M_{P}-M_{Q}$$ है, जहाँ $$M_{P}, M_{Q}$$ और $$M_{N}$$ क्रमशः $$P, Q$$ और $$N$$ के द्रव्यमान हैं। $$E_{P}$$ और $$E_{Q}$$ क्रमशः $$P$$ और $$Q$$ की गतिज ऊर्जाएं हैं। $$v_{P}$$ और $$v_{Q}$$ क्रमशः $$P$$ और $$Q$$ की गति हैं। यदि निर्वात में प्रकाश की गति $$c$$ है, तो निम्न में से कौन सा (से) कथन सही है (हैं) ?

$$x y$$-समतल पर दो सकेन्द्रित वृत्ताकार लूप (loop) चित्रानुसार रखे हैं जिनके कॉमन केंद्र मूल बिंदु (origin) पर हैं। इसमें एक की त्रिज्या $$R$$ और दूसरे की त्रिज्या $$2 R$$ है। छोटे लूप में धारा $$I_{1}$$ वामावर्त (anti-clockwise) दिशा में है एवं बड़े लूप में धारा $$I_{2}$$ दक्षिणावर्त (clockwise) दिशा में है, जहाँ $$I_{2} > 2 I_{1}$$ है $$x y$$-समतल के बिन्दु $$(x, y)$$ पर चुम्बकीय क्षेत्र (magnetic field) $$\vec{B}(x, y)$$ से परिभाषित है। निम्न में से कौन सा (से) कथन सही है (हैं) ?

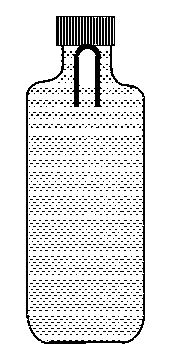
$$1 ~\mathrm{gm} / \mathrm{cc}$$ घनत्व वाले पानी से भरी एक नरम प्लास्टिक बोतल में काँच की एक परखनली (test tube) उल्टी रखी हुई है (चित्र देखें) | परखनली के अन्दर कुछ वायु (आदर्श गैस) फंसी हुई है। मोटे काँच से बनी परखनली का द्रव्यमान $$5 ~\mathrm{gm}$$ है और काँच का घनत्व $$\rho=2.5 ~\mathrm{gm} / \mathrm{cc}$$ है | आरंभ में बोतल को वायुमंडलीय दाब $$p_{0}=10^{5} \mathrm{~Pa}$$ पर बंद किया जाता है जिससे परखनली में फंसी वायु का आयतन $$v_{0}=3.3 ~\mathrm{cc}$$ है। जब नियत (constant) तापमान पर बोतल को बाहर से दबाया जाता है तो उसके अन्दर का दाब बढ़ जाता है और परखनली में प्रग्रहित (trapped) वायु का आयतन कम हो जाता है । यह पाया जाता है कि दाब $$p_{0}+\Delta p$$ पर परखनली बिना अभिविन्यास परिवर्तन के (without changing orientation) डूबने लगती है और इसमें प्रग्रहित वायु का आयतन $$v_{0}-\Delta v$$ हो जाता है। मान लीजिए $$\Delta v=X ~\mathrm{cc}$$ और $$\Delta p=Y \times 10^{3} \mathrm{~Pa}$$ है।

$$X$$ का मान __________ है।

$$1 ~\mathrm{gm} / \mathrm{cc}$$ घनत्व वाले पानी से भरी एक नरम प्लास्टिक बोतल में काँच की एक परखनली (test tube) उल्टी रखी हुई है (चित्र देखें) | परखनली के अन्दर कुछ वायु (आदर्श गैस) फंसी हुई है। मोटे काँच से बनी परखनली का द्रव्यमान $$5 ~\mathrm{gm}$$ है और काँच का घनत्व $$\rho=2.5 ~\mathrm{gm} / \mathrm{cc}$$ है | आरंभ में बोतल को वायुमंडलीय दाब $$p_{0}=10^{5} \mathrm{~Pa}$$ पर बंद किया जाता है जिससे परखनली में फंसी वायु का आयतन $$v_{0}=3.3 ~\mathrm{cc}$$ है। जब नियत (constant) तापमान पर बोतल को बाहर से दबाया जाता है तो उसके अन्दर का दाब बढ़ जाता है और परखनली में प्रग्रहित (trapped) वायु का आयतन कम हो जाता है । यह पाया जाता है कि दाब $$p_{0}+\Delta p$$ पर परखनली बिना अभिविन्यास परिवर्तन के (without changing orientation) डूबने लगती है और इसमें प्रग्रहित वायु का आयतन $$v_{0}-\Delta v$$ हो जाता है। मान लीजिए $$\Delta v=X ~\mathrm{cc}$$ और $$\Delta p=Y \times 10^{3} \mathrm{~Pa}$$ है।

$$Y$$ का मान __________ है।

एक लोलक (pendulum), द्रव्यमान $$m=0.1 \mathrm{~kg}$$ के एक गोलक (bob) और लम्बाई $$L=1.0 \mathrm{~m}$$ के एक द्रव्यमानरहित (massless) तथा न खींचने वाले (inextensible) धागे से बना है । यह एक घर्षणहीन क्षैतिज फर्श (floor) से $$H=0.9 \mathrm{~m}$$ की ऊँचाई पर एक स्थिर बिंदु से लटका हुआ है। आरंभ में गोलक, फर्श पर निलंबन बिन्दु (point of suspension) के ठीक उर्ध्वाधर नीचे स्थिरावस्था मैं है। किसी क्षण, गोलक को $$P=0.2 \mathrm{~kg}$$-$$\mathrm{m} / \mathrm{s}$$ का एक क्षैतिज आवेग (impulse) प्रदान किया जाता है। इस कारण कुछ दूरी तक फिसलने के बाद, गोलक सतह से ऊपर उठ जाता है और धागा तन जाता है (becomes taut)। गोलक के सतह से उठने के तुरंत पहले, निलंबन बिन्दु के सापेक्ष, लोलक का कोणीय संवेग (angular momentum) $$J \mathrm{~kg}$$-$$\mathrm{m}^{2} / \mathrm{s}$$ है। सतह से उठने के तुरंत बाद लोलक की गतिज ऊर्जा $$K$$ Joules है।

$$J$$ का मान _________ है।

एक लोलक (pendulum), द्रव्यमान $$m=0.1 \mathrm{~kg}$$ के एक गोलक (bob) और लम्बाई $$L=1.0 \mathrm{~m}$$ के एक द्रव्यमानरहित (massless) तथा न खींचने वाले (inextensible) धागे से बना है । यह एक घर्षणहीन क्षैतिज फर्श (floor) से $$H=0.9 \mathrm{~m}$$ की ऊँचाई पर एक स्थिर बिंदु से लटका हुआ है। आरंभ में गोलक, फर्श पर निलंबन बिन्दु (point of suspension) के ठीक उर्ध्वाधर नीचे स्थिरावस्था मैं है। किसी क्षण, गोलक को $$P=0.2 \mathrm{~kg}$$-$$\mathrm{m} / \mathrm{s}$$ का एक क्षैतिज आवेग (impulse) प्रदान किया जाता है। इस कारण कुछ दूरी तक फिसलने के बाद, गोलक सतह से ऊपर उठ जाता है और धागा तन जाता है (becomes taut)। गोलक के सतह से उठने के तुरंत पहले, निलंबन बिन्दु के सापेक्ष, लोलक का कोणीय संवेग (angular momentum) $$J \mathrm{~kg}$$-$$\mathrm{m}^{2} / \mathrm{s}$$ है। सतह से उठने के तुरंत बाद लोलक की गतिज ऊर्जा $$K$$ Joules है।

$$K$$ का मान _________ है।

एक परिपथ (circuit) में $$C ~\mu \mathrm{F}$$ धारिता (capacitance) के एक संधारित्र (capacitor) और धातु से बने एक तंतु लैंप (filament lamp) को श्रेणीक्रम में (in series) एक $$200 \mathrm{~V}, 50 \mathrm{~Hz}$$ के एक आपूर्ति स्रोत से जोड़ा गया है। तंतु लैंप में $$500 \mathrm{~W}$$ बिजली की खपत होती है, जब लैंप में विभवपात (voltage drop) $$100 \mathrm{~V}$$ है । मान लें कि इस परिपथ में कोई प्रेरकीय भार (inductive load) नहीं है। दिए गए विभवों के मान वर्ग माध्य मूल (rms) में लें। धारा और आपूर्ति वोल्टता (supply voltage) के बीच कला-कोण (phase-angle) का परिमाण $$\varphi$$ अंश (degree) है। मान लीजिए $$\pi \sqrt{3} \approx 5$$ |

$$C$$ का मान ________ है।

एक परिपथ (circuit) में $$C ~\mu \mathrm{F}$$ धारिता (capacitance) के एक संधारित्र (capacitor) और धातु से बने एक तंतु लैंप (filament lamp) को श्रेणीक्रम में (in series) एक $$200 \mathrm{~V}, 50 \mathrm{~Hz}$$ के एक आपूर्ति स्रोत से जोड़ा गया है। तंतु लैंप में $$500 \mathrm{~W}$$ बिजली की खपत होती है, जब लैंप में विभवपात (voltage drop) $$100 \mathrm{~V}$$ है । मान लें कि इस परिपथ में कोई प्रेरकीय भार (inductive load) नहीं है। दिए गए विभवों के मान वर्ग माध्य मूल (rms) में लें। धारा और आपूर्ति वोल्टता (supply voltage) के बीच कला-कोण (phase-angle) का परिमाण $$\varphi$$ अंश (degree) है। मान लीजिए $$\pi \sqrt{3} \approx 5$$ |

$$\varphi$$ का मान ________ है।

जब चुम्बकीय आघूर्ण $$m$$ को लूप के केंद्र से $$r$$ दूरी पर रखा जाता है (जैसा कि ऊपर के चित्र में दर्शाया गया है), तब लूप में प्रेरित धारा का मान निम्न में किसके समानुपाती होगा?

ऊपर दिए गये प्रक्रम द्वारा चुम्बकीय आघूर्ण $$m$$ को अनंत से लूप के केंद्र से $$r$$ दूरी पर लाने में किए गए कार्य का मान निम्न में किसके समानुपाती होगा?

$$\frac{T_{R}}{T_{0}}$$ का मान है

$$\frac{Q}{R T_{0}}$$ का मान है

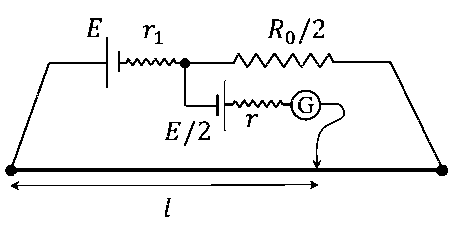
वि० वा० ब० $$(\mathrm{emf}) E$$ के एक सेल के आतंरिक प्रतिरोध $$r_{1}$$ को मापने के लिए $$R_{0}=50 ~\Omega$$ प्रतिरोध के तार वाले एक मीटर ब्रिज, एक $$R_{0} / 2$$ प्रतिरोध, वि० वा० ब० $$E / 2$$ (आतंरिक प्रतिरोध $$r$$ ) के एक अन्य सेल तथा एक धारामापी (Galvanometer) $$G$$ को चित्रानुसार प्रयोग करते हैं। यदि धारामापी में शून्य बिन्दु को मीटर ब्रिज पर $$l=72 \mathrm{~cm}$$ पर पाया जाता है, तब $$r_{1}$$ का मान __________ $$\Omega$$ होगा।

द्रव्यमान $$3 M_{S}$$ तथा $$6 M_{S}$$ के दो तारों (stars) के मध्य की दूरी $$9 R$$ है। यहाँ $$R$$ पृथ्वी व सूर्य के केन्द्रों के मध्य की दूरी है एवं $$M_{S}$$ सूर्य का द्रव्यमान है| दोनों तारे अपने कॉमन द्रव्यमान केन्द्र (common center of mass) के परितः $$n T$$ आवर्तकाल (time period) की वृत्ताकार कक्षाओं में घूमते हैं, जहाँ $$T$$ पृथ्वी द्वारा सूर्य के परिक्रमा में लगने वाला समय है। $$n$$ का मान __________ होगा।

प्रकाश विद्युत् प्रभाव (photoelectric effect) के एक प्रयोग में धातु $$\mathrm{P}, \mathrm{Q}$$ एवं $$\mathrm{R}$$ से उत्सर्जित फोटोइलेक्ट्रानों की अधिकतम गतिज ऊर्जाओं (kinetic energies) के बीच का सम्बन्ध $$E_{P}=2 E_{Q}=2 E_{R}$$ है। इस प्रयोग में $$\mathrm{P}$$ एवं $$\mathrm{Q}$$ के लिए एकवर्णी (monochromatic) प्रकाश स्रोत तथा $$\mathrm{R}$$ के लिए एक अन्य एकवर्णी प्रकाश स्रोत का उपयोग किया जाता है। $$\mathrm{P}, \mathrm{Q}$$ एवं $$\mathrm{R}$$ के कार्य फलनों (work functions) के मान क्रमशः $$4.0 ~\mathrm{eV}, 4.5 ~\mathrm{eV}$$ तथा $$5.5 ~\mathrm{eV}$$ हैं। धातु $$\mathrm{R}$$ पर आपतित (incident) प्रकाश के फोटान की ऊर्जा ($$\mathrm{eV}$$ में) ___________ होगी।