JEE Advance - Physics Hindi (2018 - Paper 1 Offline)
1
दो सदिश $$\overrightarrow A $$ और $$\overrightarrow B $$ को परिभाषित किया गया है $$\overrightarrow A $$ $$=$$ $$a\widehat i$$ और $$\overrightarrow B = a$$ $$\left( {\cos \,\omega T\widehat i + \sin \,\omega t\,\widehat j} \right),$$ जहां $$a$$ एक स्थिरांक है और $$\omega = \pi /6\,\,rad{s^{ - 1}}$$ है। यदि $$\left| {\overrightarrow A + \overrightarrow B } \right| = \sqrt 3 \left| {\overrightarrow A - \overrightarrow B } \right|$$ समय $$t = \tau $$ पर पहली बार के लिए, तो $$\tau $$ का मान, सेकंड में, ______________ है।
Answer
2
2
मान लें एक द्रव्यमान $$1.0$$ $$kg$$ का शरीर $$t=0$$ पर उत्पत्ति पर विश्राम कर रहा है। एक बल $$\overrightarrow F = \left( {\alpha t \widehat i + \beta \widehat j} \right)$$ शरीर पर लागू होता है, जहाँ $$\alpha = 1.0N{s^{ - 1}}$$ और $$\beta = 1.0\,N$$ है। $$t=1.0s$$ के समय उत्पत्ति के बारे में शरीर पर कार्य करने वाला घूर्णन $$\overrightarrow \tau $$ है। निम्नलिखित में से कौन सा कथन सत्य है?
Answer
A
C
3
आधारिक त्रिज्या $$r$$ वाली एक समान केशिका नली को पानी से भरे किसी बीकर में लंबवत् रूप से डुबोया गया है। पानी बीकर में जल सतह के ऊपर केशिका नली में $$h$$ की ऊँचाई तक उठता है। जल का पृष्ठ तनाव $$\sigma$$ है। केशिका नली की दीवार और पानी के बीच संपर्क कोण $$\theta$$ है। मेनिस्कस में पानी के द्रव्यमान की उपेक्षा करें। निम्नलिखित में से कौन सा कथन सही है?
Answer
A
C
4
दो अनंत लंबे सीधे तार $$xy$$-समतल में $$x = \pm R$$ लाइनों के साथ स्थित हैं। $$x = + R$$ पर स्थित तार एक स्थिर धारा $${I_1}$$ और $$x=-R$$ पर स्थित तार एक स्थिर धारा $${I_2}$$ वहन करता है। $$R$$ के त्रिज्या का एक गोलाकार लूप $$\left( {0,0,\sqrt 3 R} \right)$$ पर अपने केंद्र के साथ निलंबित है और $$xy$$-समतल के समानांतर एक समतल में है। यह लूप ऊपर से देखे जाने पर घड़ी की दिशा में एक स्थिर धारा $$I$$ वहन करता है। तार में धारा सकारात्मक मानी जाती है यदि यह $$ + \widehat j$$ दिशा में है। निम्नलिखित कथनों में से कौन-सा/से कथन चुंबकीय क्षेत्र $$\overrightarrow B $$ के बारे में सही है / हैं?
Answer
A
B
D
5
दो व्यक्ति एक क्षैतिज सीधी रेखा के साथ एक ही दिशा में चल रहे हैं। सामने वाला व्यक्ति $$1.0\,m{s^{ - 1}}$$ की गति से चलता है और पीछे वाला व्यक्ति $$2.0\,m{s^{ - 1}}$$ की गति से चलता है। तीसरा व्यक्ति $$12$$ $$m$$ की ऊँचाई पर उसी क्षैतिज रेखा के ऊपर खड़ा है, जिससे सभी तीन व्यक्ति एक ऊर्ध्वाधर समतल में होते हैं। चलने वाले दोनों व्यक्ति समान सीटी बजा रहे हैं जो $$1430$$ $$Hz$$ की ध्वनि उत्पन्न करते हैं। हवा में ध्वनि की गति $$330\,m{s^{ - 1}}$$ है। उस समय, जब चलने वाले व्यक्ति $$10$$ $$m$$ अलग होते हैं, स्थिर व्यक्ति उनसे समान दूरी पर होता है। $$Hz$$ में स्थिर व्यक्ति द्वारा उस समय सुनी गई बीट्स की आवृत्ति __________ है।
Answer
5
6
एक रिंग और डिस्क प्रारंभिक रूप से विश्राम स्थिति में, एक झुके हुए तल के शीर्ष पर एक दूसरे के पास, $$60^ \circ$$ क्षैतिज से कोण बनाते हुए स्थित थे। वे एक ही समय में बिना फिसले सबसे छोटे पथ के साथ रोल करना शुरू करते हैं। यदि उनकी जमीन पर पहुंचने के समय में अंतर $$\left( {2 - \sqrt 3 } \right)/\sqrt {10} \,\,s,$$ है, तो झुके हुए तल के शीर्ष की ऊँचाई, मीटर्स में ______________ है। मान लें $$g = 10\,\,m{s^{ - 2}}.$$
Answer
0.75
7
एक स्प्रिंग-ब्लॉक प्रणाली घर्षण रहित फर्श पर आराम कर रही है जैसा कि चित्र में दिखाया गया है। स्प्रिंग स्थिरांक $$2.0\,N{m^{ - 1}}$$ और ब्लॉक का द्रव्यमान $$2.0$$ $$kg$$ है। स्प्रिंग के द्रव्यमान को नजरअंदाज करें। प्रारंभ में स्प्रिंग एक असंवर्धित स्थिति में है। $$1.0$$ $$kg$$ द्रव्यमान का एक और ब्लॉक $$2.0$$ $$m{s^{ - 1}}$$ की गति से पहले ब्लॉक से टकराता है। टक्कर ऐसी होती है कि $$2.0$$ $$kg$$ का ब्लॉक दीवार से नहीं टकराता। स्प्रिंग के पहली बार असंवर्धित स्थिति में वापस आने पर दो ब्लॉकों के बीच की दूरी, मीटरों में, __________ है।
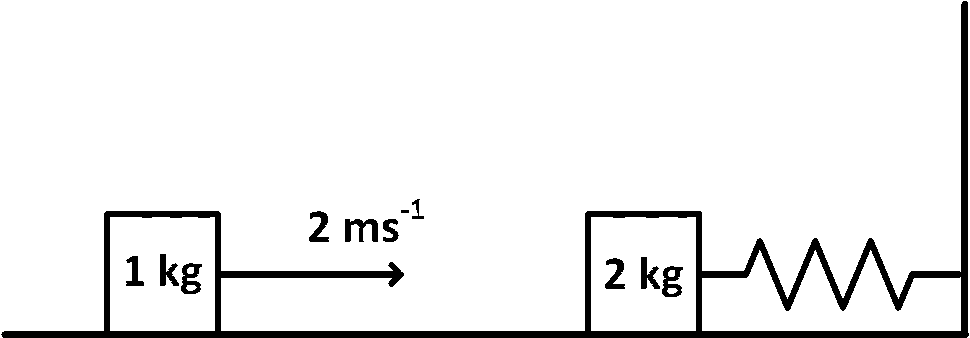

Answer
2.09
8
निम्नलिखित चित्र में, स्विच $${S_1}$$ और $${S_2}$$ को $$t=0$$ पर एक साथ बंद किया जाता है और सर्किट में धारा प्रवाहित होने लगती है। दोनों बैटरियों के विद्युत वाहक बल (emf) का परिमाण समान है और ध्रुवताएं चित्र में दर्शाई गई हैं। इंडक्टरों के बीच पारस्परिक प्रेरण का ध्यान न दें। मध्य के तार में धारा $$I$$ अधिकतम परिमाण $${I_{\max }}$$ पर समय $$t = \tau$$ पर पहुंचती है। निम्नलिखित में से कौन सा (कौन से) वक्तव्य सही है (हैं)?


Answer
B
D
9
तीन समान धारिता वाले संधारित्र $${C_1},{C_2}$$ और $${C_3}$$ की धारिता $$1.0\,\mu F$$ (माइक्रोफैराड) है और वे प्रारंभ में अप्रयुक्त होते हैं। उन्हें चित्र में दिखाए अनुसार परिपथ में जोड़ा जाता है और फिर $${C_1}$$ को सापेक्ष परमीविट्टी $${\varepsilon _r}$$ के एक डाइलेक्ट्रिक पदार्थ से पूरी तरह से भरा जाता है। सेल विद्युत प्रेरक बल $$\left( {emf} \right)\,\,{V_0} = 8V.$$ पहले स्विच $${S_1}$$ को बंद किया जाता है जबकि स्विच $${S_2}$$ को खुला रखा जाता है। जब संधारित्र $${C_3}$$ पूरी तरह से चार्ज हो जाता है, तो $${S_1}$$ को खोल दिया जाता है और $${S_2}$$ को एक ही समय में बंद कर दिया जाता है। जब सभी संधारित्र संतुलन में पहुँच जाते हैं, तो $${C_3}$$ पर आवेश $$5\,\mu C$$ होता है। $${\varepsilon _r}$$ का मान _________________.
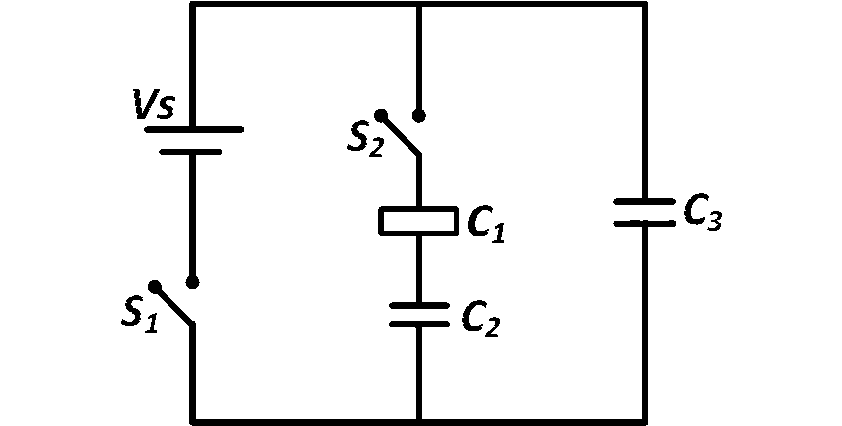

Answer
1.50
10
मान लें एक द्रव्यमान $$1.0$$ $$kg$$ का शरीर $$t=0$$ पर उत्पत्ति पर विश्राम कर रहा है। एक बल $$\overrightarrow F = \left( {\alpha t \widehat i + \beta \widehat j} \right)$$ शरीर पर लागू होता है, जहाँ $$\alpha = 1.0N{s^{ - 1}}$$ और $$\beta = 1.0\,N$$ है। $$t=1.0s$$ के समय उत्पत्ति के बारे में शरीर पर कार्य करने वाला घूर्णन $$\overrightarrow \tau $$ है। निम्नलिखित में से कौन सा कथन सत्य है?
Answer
A
C
11
आधारिक त्रिज्या $$r$$ वाली एक समान केशिका नली को पानी से भरे किसी बीकर में लंबवत् रूप से डुबोया गया है। पानी बीकर में जल सतह के ऊपर केशिका नली में $$h$$ की ऊँचाई तक उठता है। जल का पृष्ठ तनाव $$\sigma$$ है। केशिका नली की दीवार और पानी के बीच संपर्क कोण $$\theta$$ है। मेनिस्कस में पानी के द्रव्यमान की उपेक्षा करें। निम्नलिखित में से कौन सा कथन सही है?
Answer
A
C
12
दो अनंत लंबे सीधे तार $$xy$$-समतल में $$x = \pm R$$ लाइनों के साथ स्थित हैं। $$x = + R$$ पर स्थित तार एक स्थिर धारा $${I_1}$$ और $$x=-R$$ पर स्थित तार एक स्थिर धारा $${I_2}$$ वहन करता है। $$R$$ के त्रिज्या का एक गोलाकार लूप $$\left( {0,0,\sqrt 3 R} \right)$$ पर अपने केंद्र के साथ निलंबित है और $$xy$$-समतल के समानांतर एक समतल में है। यह लूप ऊपर से देखे जाने पर घड़ी की दिशा में एक स्थिर धारा $$I$$ वहन करता है। तार में धारा सकारात्मक मानी जाती है यदि यह $$ + \widehat j$$ दिशा में है। निम्नलिखित कथनों में से कौन-सा/से कथन चुंबकीय क्षेत्र $$\overrightarrow B $$ के बारे में सही है / हैं?
Answer
A
B
D
13
$$xy$$-समतल में, क्षेत्र $$y > 0$$ में एक समान चुंबकीय क्षेत्र $${B_1}\widehat k$$ है और क्षेत्र $$y < 0$$ में एक अन्य समान चुंबकीय क्षेत्र $${B_2}\widehat k$$ है। एक धनात्मक आवेशित कण को उत्पत्ति बिंदु से धनात्मक $$y$$-अक्ष के साथ $${v_0} = \pi \,m{s^{ - 1}}$$ की गति के साथ प्रक्षेपित किया जाता है $$t=0$$ पर, जैसा कि चित्र में दिखाया गया है। इस समस्या में गुरुत्वाकर्षण की उपेक्षा करें। मान लें कि $$t=T$$ वह समय है जब कण पहली बार नीचे से $$x$$-अक्ष को पार करता है। यदि $${B_2} = 4{B_1},$$ कण की औसत गति, $$m{s^{ - 1}}$$ में, अंतराल $$T$$ के दौरान $$x$$-अक्ष के साथ ___________ है।

Answer
2
14
विद्युतचुम्बकीय सिद्धांत में, विद्युत और चुम्बकीय घटनाएं आपस में संबंधित होती हैं। इसलिए, विद्युत और चुम्बकीय मात्राओं के आयाम भी एक दूसरे से संबंधित होने चाहिए। नीचे दिए गए सवालों में, $$[E]$$ और $$[B]$$ क्रमशः विद्युत क्षेत्र और चुम्बकीय क्षेत्र के आयामों को अभिव्यक्त करते हैं, जबकि $$\left[ {{\varepsilon _0}} \right]$$ और $$\left[ {{\mu _0}} \right]$$ क्रमशः मुक्त स्थान की विद्युत निरपेक्षता और चुंबकीय पारगम्यता के आयामों को अभिव्यक्त करते हैं। $$\left[ L \right]$$ और $$\left[ T \right]$$ क्रमशः लंबाई और समय के आयाम हैं। सभी मात्राएँ $$SI$$ इकाइयों में दी गई हैं।
$$\left[ {{\varepsilon _0}} \right]$$ और $$\left[ {{\mu _0}} \right]$$ के बीच का संबंध है
$$\left[ {{\varepsilon _0}} \right]$$ और $$\left[ {{\mu _0}} \right]$$ के बीच का संबंध है
Answer
(D)
$$\left[ {{\mu _0}} \right] = {\left[ {{\varepsilon _0}} \right]^{ - 1}}{\left[ L \right]^{ - 2}}{\left[ T \right]^2}$$
15
यदि सभी स्वतंत्र मात्राओं में माप त्रुटियां ज्ञात हैं, तो किसी भी निर्भर मात्रा में त्रुटि को निर्धारित करना संभव है। इसे श्रृंखला विस्तार का उपयोग करके और त्रुटि की पहली शक्ति पर विस्तार को काटकर किया जाता है। उदाहरण के लिए, $$z = x/y$$ संबंध को मानें। यदि $$x,y$$ और $$z$$ में त्रुटियां $$\Delta x,\Delta y$$ और $$\Delta z,$$ क्रमशः हैं, तो
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
$${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}$$ का श्रृंखला विस्तार, $$\Delta y/y$$ में पहली शक्ति पर $$1 \pm \left( {\Delta y/y} \right)$$ होता है। स्वतंत्र वेरिएबल्स में सापेक्ष त्रुटियां हमेशा जोड़ी जाती हैं। इसलिए $$z$$ में त्रुटि होगी
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
ऊपर दी गई व्युत्पत्ति यह मानती है कि $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ इसलिए, इन मात्राओं की उच्च शक्तियों को नजरअंदाज किया जाता है।
एक प्रयोग में रेडियोधर्मी नाभिकों की प्रारंभिक संख्या $$3000$$ है। पाया जाता है कि पहले $$1.0s$$ में $$1000 \pm 40$$ नाभिक क्षय होते हैं। $$\left| x \right| < < 1$$ के लिए। $$\ln \left( {1 + x} \right) = x$$ $$x$$ में पहली शक्ति तक। $$\lambda ,$$ के क्षय स्थिरांक $$\lambda ,$$ ($$s^{-1}$$) के निर्धारण में त्रुटि $$\Delta \lambda ,$$ है
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
$${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}$$ का श्रृंखला विस्तार, $$\Delta y/y$$ में पहली शक्ति पर $$1 \pm \left( {\Delta y/y} \right)$$ होता है। स्वतंत्र वेरिएबल्स में सापेक्ष त्रुटियां हमेशा जोड़ी जाती हैं। इसलिए $$z$$ में त्रुटि होगी
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
ऊपर दी गई व्युत्पत्ति यह मानती है कि $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ इसलिए, इन मात्राओं की उच्च शक्तियों को नजरअंदाज किया जाता है।
एक प्रयोग में रेडियोधर्मी नाभिकों की प्रारंभिक संख्या $$3000$$ है। पाया जाता है कि पहले $$1.0s$$ में $$1000 \pm 40$$ नाभिक क्षय होते हैं। $$\left| x \right| < < 1$$ के लिए। $$\ln \left( {1 + x} \right) = x$$ $$x$$ में पहली शक्ति तक। $$\lambda ,$$ के क्षय स्थिरांक $$\lambda ,$$ ($$s^{-1}$$) के निर्धारण में त्रुटि $$\Delta \lambda ,$$ है
Answer
(C)
$$0.02$$
16
यदि सभी स्वतंत्र मदों में मापन त्रुटियाँ ज्ञात हों, तो किसी निर्भर मद में त्रुटि का निर्धारण करना संभव है। यह श्रेणी विस्तार का उपयोग करके किया जाता है और त्रुटि की पहली शक्ति पर विस्तार को काटता है। उदाहरण के लिए, संबंध देखें $$z = x/y.$$ यदि $$x,y$$ और $$z$$ में त्रुटियाँ $$\Delta x,\Delta y$$ और $$\Delta z$$ क्रमशः होती हैं, तो
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
$$$${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}$$$ का श्रेणी विस्तार, $$\Delta y/y$$ की पहली शक्ति के लिए, $$1 \pm \left( {\Delta y/y} \right)$$ है। स्वतंत्र चर में आनुपातिक त्रुटियाँ हमेशा जोड़ी जाती हैं। इसलिए $$z$$ में त्रुटि
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
उपरोक्त व्युत्पन्न दौरान यह मान लिया जाता है कि $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ इसलिए, इन मात्राओं के उच्च शक्तियों की उपेक्षा की जाती है।
मान लें कि अनुपात $$r = {{\left( {1 - a} \right)} \over {1 + a}}$$ को एक विमाहीन मात्रा $$a$$ मापकर निर्धारित किया जाता है। यदि $$a$$ के मापन में त्रुटि $$\Delta a\left( {\Delta a/a < < 1.} \right.$$ है, तो $$r$$ को निर्धारित करने में त्रुटि $$\Delta r$$ है?
$$$z \pm \Delta z = {{x \pm \Delta x} \over {y \pm \Delta y}} = {x \over y}\left( {1 \pm {{\Delta x} \over x}} \right){\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}.$$$
$$$${\left( {1 \pm {{\Delta y} \over y}} \right)^{ - 1}}$$$ का श्रेणी विस्तार, $$\Delta y/y$$ की पहली शक्ति के लिए, $$1 \pm \left( {\Delta y/y} \right)$$ है। स्वतंत्र चर में आनुपातिक त्रुटियाँ हमेशा जोड़ी जाती हैं। इसलिए $$z$$ में त्रुटि
$$$\Delta z = z\left( {{{\Delta x} \over x} + {{\Delta y} \over y}} \right).$$$
उपरोक्त व्युत्पन्न दौरान यह मान लिया जाता है कि $$\Delta x/x < < 1,$$ $$\Delta y/y < < 1.$$ इसलिए, इन मात्राओं के उच्च शक्तियों की उपेक्षा की जाती है।
मान लें कि अनुपात $$r = {{\left( {1 - a} \right)} \over {1 + a}}$$ को एक विमाहीन मात्रा $$a$$ मापकर निर्धारित किया जाता है। यदि $$a$$ के मापन में त्रुटि $$\Delta a\left( {\Delta a/a < < 1.} \right.$$ है, तो $$r$$ को निर्धारित करने में त्रुटि $$\Delta r$$ है?
Answer
(B)
$${{2\Delta a} \over {{{\left( {1 + a} \right)}^2}}}$$
17
विद्युतचुम्बकीय सिद्धांत में, विद्युत और चुम्बकीय घटनाएं एक दूसरे से संबंधित होती हैं। इसलिए, विद्युत और चुम्बकीय मात्राओं के आयाम भी एक दूसरे से संबंधित होने चाहिए। नीचे दिए गए प्रश्नों में, $$[E]$$ और $$[B]$$ विद्युत और चुम्बकीय क्षेत्रों के आयामों को सूचित करते हैं, जबकि $$\left[ {{\varepsilon _0}} \right]$$ और $$\left[ {{\mu _0}} \right]$$ मुक्त स्थान की विसर्पिता और पारगम्यता के आयामों को सूचित करते हैं। $$\left[ L \right]$$ और $$\left[ T \right]$$ क्रमशः लंबाई और समय के आयाम हैं। सभी मात्राएं $$SI$$ इकाइयों में दी गई हैं।
$$[E]$$ और $$[B]$$ के बीच संबंध है
$$[E]$$ और $$[B]$$ के बीच संबंध है
Answer
(C)
$$\left[ E \right] = \left[ B \right]\left[ L \right]{\left[ T \right]^{ - 1}}$$
18
किसी निश्चित बिन्दु $$O$$ से दूरी $$r$$ पर स्थित द्रव्यमान $$m$$ वाले कण की स्थितिज ऊर्जा $$V\left( r \right) = k{r^2}/2$$ द्वारा दी गई है, जहां $$k$$ सकारात्मक नियतांक है जिसके पास उपयुक्त आयाम हैं। यह कण बिन्दु $$O$$ के चारों ओर $$R$$ त्रिज्या की वृत्ताकार कक्षा में गति कर रहा है। यदि $$v$$ कण का वेग और $$L$$ बिन्दु $$O$$ के बारे में इसका कोणीय संवेग है, तो निम्नलिखित वक्तव्यों में से कौन सा (कौन से) सही है (हैं)?
Answer
B
C

