एक बिंदु चार्ज $$+Q$$ एक काल्पनिक अर्धगोलाकार सतह की त्रिज्या $$R$$ के ठीक बाहर रखा गया है जैसा कि चित्र में दिखाया गया है। निम्नलिखित में से कौन सा/से कथन सही है/हैं?

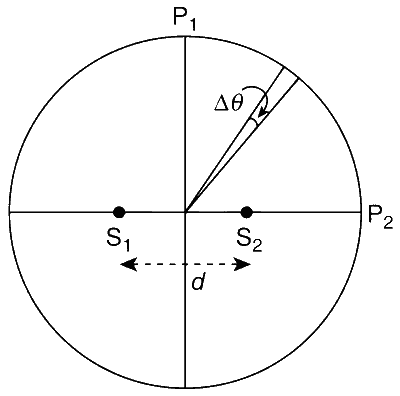
दो संगत एकरंगी बिंदु स्रोत $${S_1}$$ और $${S_2}$$ जिनकी तरंगदैर्ध्य $$\lambda = 600\,nm$$ हैं, वृत्त के केंद्र के किसी भी तरफ समान रूप से रखे जाते हैं, जैसे कि दिखाया गया है। स्रोत एक दूसरे से $$d=1.8$$ $$mm$$ की दूरी पर स्थित हैं। यह व्यवस्था वृत्त की परिधि पर वैकल्पिक उज्ज्वल और अंधेरे धब्बों के रूप में हस्तक्षेप धारियां उत्पन्न करती है। दो लगातार उज्ज्वल धब्बों के बीच कोणीय अंतर $$\Delta \theta$$ है। निम्नलिखित विकल्पों में से कौन सा/से सही है/हैं?

तीन टर्मिनल $$X,Y$$ और $$Z$$ पर तात्कालिक वोल्टेज इस प्रकार हैं

$${V_x} = {V_0}\,\sin \,\omega t,$$

$${V_Y} = {V_0}\,\sin $$ $$\left( {\omega t + {{2\pi } \over 3}} \right)$$

और $$Vz = {V_0}\sin \left( {\omega t + {{4\pi } \over 3}} \right)$$

एक आदर्श वोल्टमीटर $$rms$$ मान के अंतर को मापने के लिए कॉन्फ़िगर किया गया है। यह बिंदुओं $$X$$ और $$Y$$ के बीच और फिर $$Y$$ और $$Z$$ के बीच जोड़ा जाता है। वोल्टमीटर की रीडिंग्स इस प्रकार होंगी

एक समान चुम्बकीय क्षेत्र $$B$$ $$x=0$$ और $$x = {{3R} \over 2}$$ (चित्र में क्षेत्र $$2$$) के बीच के क्षेत्र में विद्यमान है और कागज के तल पर सामान्य रूप से इंगित करता है। एक कण जिसका आवेश $$+Q$$ और हेलन $$p$$ है, जो $$x$$-अक्ष के साथ निर्देशित है, क्षेत्र $$2$$ में क्षेत्र $$1$$ से प्रवेश करता है बिंदु $${P_1}\left( y \right) = - R)$$ पर। निम्नलिखित विकल्पों में से कौन सा सही है/हैं?

एक व्यक्ति एक पत्थर गिराने और कुएँ की तली के साथ प्रभाव की ध्वनि प्राप्त करने के बीच का समय अंतराल मापकर किसी कुएँ की गहराई मापता है। समय की उसकी माप में त्रुटि $$\delta T = 0.01$$ सेकंड है और वह कुएँ की गहराई $$L=20$$ मीटर मापता है। गुरुत्वाकर्षण त्वरण $$g = 10m{s^{ - 2}}$$ और ध्वनि की वृद्धि $$300$$ $$m{s^{ - 1}}$$ लें। तब मापन में अंशदायी त्रुटि, $$\delta L/L,$$ के निकटतम है

एक रॉकेट को पृथ्वी की सतह से सूर्य की ओर सामान्य दिशा में, पृथ्वी और सूर्य को जोड़ने वाली रेखा के साथ प्रक्षेपित किया गया है। सूर्य पृथ्वी से $$3 \times 10{}^5$$ गुना भारी है और पृथ्वी की त्रिज्या से $$2.5 \times {10^4}$$ गुना अधिक दूरी पर स्थित है। पृथ्वी के गुरुत्वाकर्षण क्षेत्र से बचने की वेग $${V_c} = 11.2 km{s^{-1}}$$ है। सूर्य-पृथ्वी प्रणाली से बाहर जाने के लिए रॉकेट के लिए न्यूनतम प्रारंभिक वेग $$\left( {{v_s}} \right)$$ सबसे करीब है (पृथ्वी के घूर्णन और क्रांति और किसी अन्य ग्रह की उपस्थिति को नजरअंदाज करें)

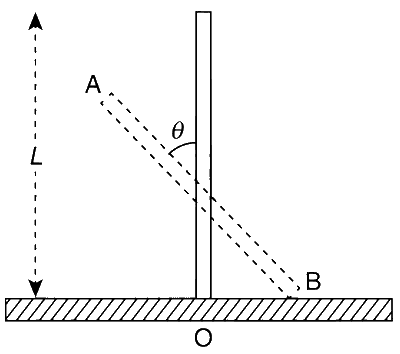
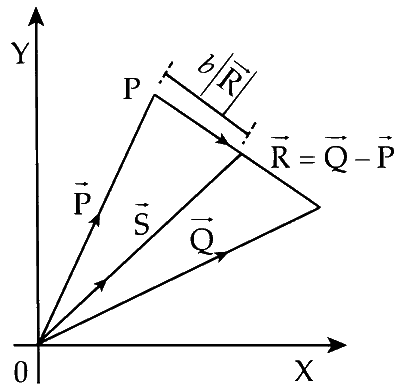
तीन सदिश $$\overrightarrow P ,\overrightarrow Q $$ और $$\overrightarrow R $$ चित्र में दिखाए गए हैं। मान लें कि $$S$$ सदिश $$\overrightarrow R$$ पर कोई बिंदु है। बिंदुओं $$P$$ और $$S$$ के बीच की दूरी $$b\left| {\overrightarrow R } \right|$$ है। सदिश $$\overrightarrow P ,\overrightarrow Q $$ और $$\overrightarrow S$$ के बीच सामान्य संबंध है :

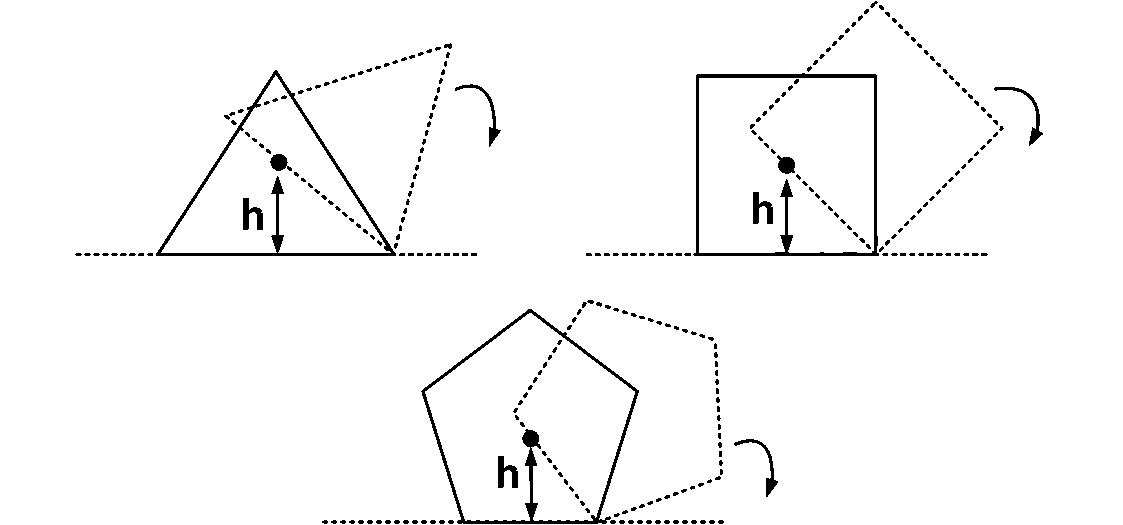
नियमित बहुभुजों पर विचार करें जिनमें पक्षों की संख्या $$n=3,4,5....$$ है जैसा कि चित्र में दिखाया गया है। सभी बहुभुजों का केंद्र मास का ऊंचाई $$h$$ भूमि से है। वे अग्रणी शीर्ष (leading vertex) के बारे में एक क्षैतिज सतह पर बिना फिसले और बिना पर्ची रोल करते हैं जैसा कि दर्शाया गया है। प्रत्येक बहुभुज के लिए केंद्र मास की लोकेशन में अधिकतम वृद्धि $$\Delta $$ है। तब $$\Delta $$ का $$n$$ और $$h$$ पर निर्भरता है

एक सममित तारांकित आकृति प्रवाहकीय तार लूप में निरंतर प्रवाह $$\rm I$$ बह रहा है जैसा कि चित्र में दिखाया गया है। तारांकित आकृति के व्यास के विपरीत कोनों के बीच की दूरी $$4a$$ है। लूप के केंद्र पर चुंबकीय क्षेत्र की परिमाण है

एक फोटोइलेक्ट्रिक सामग्री जिसकी कार्य-फंक्शन $${\phi _0}$$ है, को $$\lambda \left( {\lambda < {{he} \over {{\phi _0}}}} \right)$$ तरंगदैर्ध्य की रोशनी से प्रकाशित किया जाता है। सबसे तेज फोटोइलेक्ट्रॉन की एक de-Broglie तरंगदैर्ध्य $${\lambda _d}$$ है। घटना रोशनी की तरंगदैर्ध्य में परिवर्तन $$\Delta \lambda $$ में, $$\Delta {\lambda _d}$$ में परिवर्तन $${\lambda _d}$$ होता है। तब अनुपात $$\Delta {\lambda _d}/\Delta \lambda $$ किसके अनुपाती है?

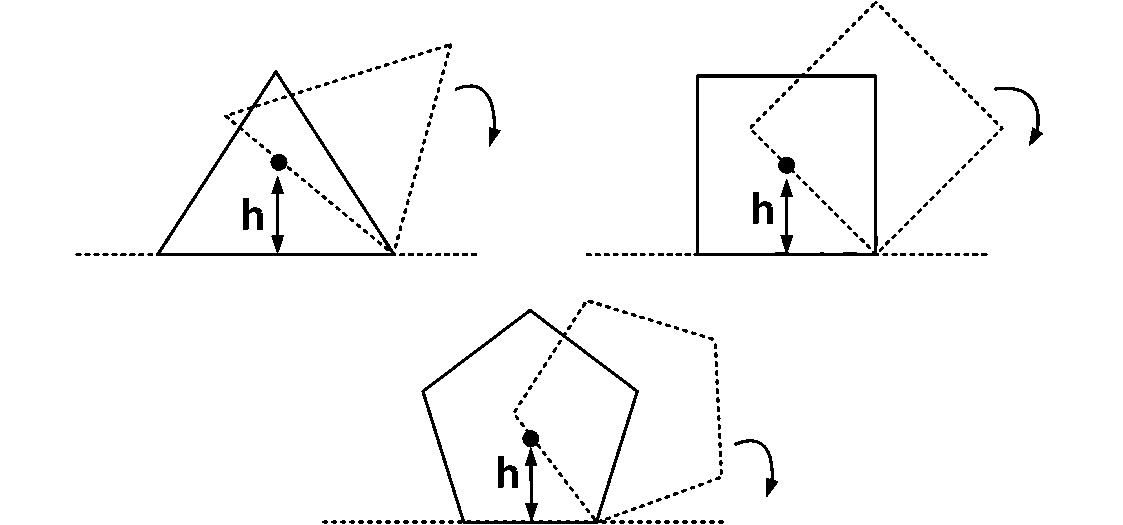
नियमित बहुभुजों पर विचार करें जिनमें पक्षों की संख्या $$n=3,4,5....$$ है जैसा कि चित्र में दिखाया गया है। सभी बहुभुजों का केंद्र मास का ऊंचाई $$h$$ भूमि से है। वे अग्रणी शीर्ष (leading vertex) के बारे में एक क्षैतिज सतह पर बिना फिसले और बिना पर्ची रोल करते हैं जैसा कि दर्शाया गया है। प्रत्येक बहुभुज के लिए केंद्र मास की लोकेशन में अधिकतम वृद्धि $$\Delta $$ है। तब $$\Delta $$ का $$n$$ और $$h$$ पर निर्भरता है

एक तात्कालिक त्रिज्या R का एक विस्तारशील गोला मानें जिसकी कुल द्रव्यमान स्थिर रहता है। विस्तार इस प्रकार का है कि तात्कालिक घनत्व $$\rho $$ सम्पूर्ण मात्रा में समान रहता है। घनत्व $$\left( {{1 \over \rho } {{d\rho } \over {dt}}} \right)$$ में आंशिक परिवर्तन की दर स्थिर है। विस्तारशील गोले के सतह पर किसी भी बिंदु का वेग $$v$$ किसके अनुपात में है

लंबाई के एक कठोर समान पट्टी $$AB$$ को उसकी लंबवत स्थिति से एक घर्षण रहित फर्श पर फिसलते हुए दिखाया गया है (जैसा कि चित्र में दिखाया गया है)। किसी समय पर पट्टी द्वारा लंबवत स्थिति के साथ बनाए गए कोण को $$\theta$$ मानें। इसके गति के बारे में निम्नलिखित में से कौन से कथन सही हैं?

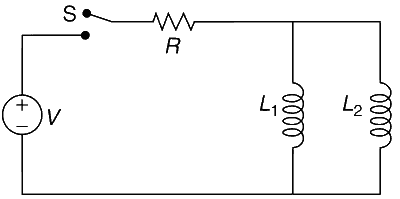
एक स्थिर वोल्टेज स्रोत $$V$$ को प्रतिरोध $$R$$ और दो आदर्श इंडक्टर $$L_1$$ और $$L_2$$ के साथ एक स्विच $$S$$ के माध्यम से जोड़ा गया है जैसा कि चित्र में दिखाया गया है। दो इंडक्टरों के बीच कोई पारस्परिक प्रेरण नहीं है। स्विच $$S$$ प्रारंभ में खुला है। $$t = 0$$ पर, स्विच बंद किया जाता है और करंट बहने लगता है। निम्नलिखित विकल्पों में से कौन सा सही है?

प्रक्रिया 1 में, संधारित्र में संग्रहीत ऊर्जा E_C और प्रतिरोध के पार अवशोषित गर्मी E_D निम्नलिखित रूप में संबंधित हैं

प्रक्रिया 2 में, प्रतिरोध R के पार पूरी अवशोषित ऊर्जा E_D है

रिंग की कुल गतिज ऊर्जा है

न्यूनतम $$\omega$$₀ का मान जिसके नीचे रिंग नीचे गिर जाएगी वह है