JEE Advance - Physics Hindi (2017 - Paper 2 Offline - No. 17)
कोई व्यक्ति अपनी उंगली की नोक के पास एक वृत्ताकार रिंग (द्रव्यमान M और त्रिज्या R) को घुमाता है जैसा कि चित्र 1 में दिखाया गया है। इस प्रक्रिया में उंगली कभी भी रिंग की आंतरिक परिधि से संपर्क नहीं खोती है। उंगली द्वारा खींची गई रेखा एक शंकु की सतह को दर्शाती है, जैसा कि बिंदीदार रेखा द्वारा दिखाया गया है। वह बिंदु जहां रिंग और उंगली का संपर्क होता है, उसकी घुमावदार पथ की त्रिज्या r है। उंगली $$\omega$$0 कोणीय वेग के साथ घूमती है। घूर्णन रिंग बिना स्लिप के छोटे वृत्त के बाहरी भाग पर लुढ़कती है, जिसे रिंग और उंगली का संपर्क बिंदु बताता है (चित्र 2)। रिंग और उंगली के बीच घर्षण गुणांक $$\mu$$ है और गुरुत्वाकर्षण त्वरण g है।
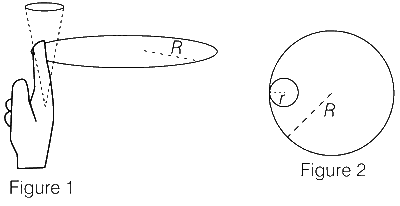

कोई व्यक्ति अपनी उंगली की नोक के पास एक वृत्ताकार रिंग (द्रव्यमान M और त्रिज्या R) को घुमाता है जैसा कि चित्र 1 में दिखाया गया है। इस प्रक्रिया में उंगली कभी भी रिंग की आंतरिक परिधि से संपर्क नहीं खोती है। उंगली द्वारा खींची गई रेखा एक शंकु की सतह को दर्शाती है, जैसा कि बिंदीदार रेखा द्वारा दिखाया गया है। वह बिंदु जहां रिंग और उंगली का संपर्क होता है, उसकी घुमावदार पथ की त्रिज्या r है। उंगली $$\omega$$0 कोणीय वेग के साथ घूमती है। घूर्णन रिंग बिना स्लिप के छोटे वृत्त के बाहरी भाग पर लुढ़कती है, जिसे रिंग और उंगली का संपर्क बिंदु बताता है (चित्र 2)। रिंग और उंगली के बीच घर्षण गुणांक $$\mu$$ है और गुरुत्वाकर्षण त्वरण g है।


कोई व्यक्ति अपनी उंगली की नोक के पास एक वृत्ताकार रिंग (द्रव्यमान M और त्रिज्या R) को घुमाता है जैसा कि चित्र 1 में दिखाया गया है। इस प्रक्रिया में उंगली कभी भी रिंग की आंतरिक परिधि से संपर्क नहीं खोती है। उंगली द्वारा खींची गई रेखा एक शंकु की सतह को दर्शाती है, जैसा कि बिंदीदार रेखा द्वारा दिखाया गया है। वह बिंदु जहां रिंग और उंगली का संपर्क होता है, उसकी घुमावदार पथ की त्रिज्या r है। उंगली $$\omega$$0 कोणीय वेग के साथ घूमती है। घूर्णन रिंग बिना स्लिप के छोटे वृत्त के बाहरी भाग पर लुढ़कती है, जिसे रिंग और उंगली का संपर्क बिंदु बताता है (चित्र 2)। रिंग और उंगली के बीच घर्षण गुणांक $$\mu$$ है और गुरुत्वाकर्षण त्वरण g है।


रिंग की कुल गतिज ऊर्जा है
$$M\omega _0^2{(R - r)^2}$$
$${1 \over 2}M\omega _0^2{(R - r)^2}$$
$$M\omega _0^2{R^2}$$
$${1 \over 2}M\omega _0^2[{(R - r)^2} + {R^2}]$$
Comments (0)


