JEE Advance - Physics Hindi (2017 - Paper 2 Offline - No. 8)
नियमित बहुभुजों पर विचार करें जिनमें पक्षों की संख्या $$n=3,4,5....$$ है जैसा कि चित्र में दिखाया गया है। सभी बहुभुजों का केंद्र मास का ऊंचाई $$h$$ भूमि से है। वे अग्रणी शीर्ष (leading vertex) के बारे में एक क्षैतिज सतह पर बिना फिसले और बिना पर्ची रोल करते हैं जैसा कि दर्शाया गया है। प्रत्येक बहुभुज के लिए केंद्र मास की लोकेशन में अधिकतम वृद्धि $$\Delta $$ है। तब $$\Delta $$ का $$n$$ और $$h$$ पर निर्भरता है
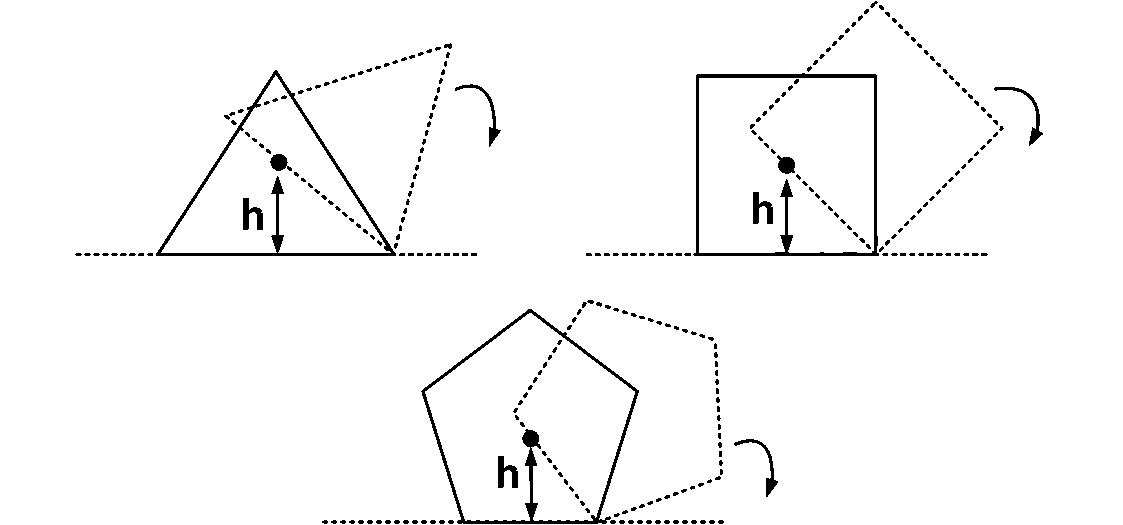

$$\Delta = h{\sin ^2}\left( {{\pi \over n}} \right)$$
$$\Delta = h\left( {{1 \over {\cos \left( {{\pi \over n}} \right)}} - 1} \right)$$
$$\Delta = h\sin \left( {{{2\pi } \over n}} \right)$$
$$\Delta = h\,{\tan ^2}\left( {{\pi \over {2n}}} \right)$$
Comments (0)


