JEE Advance - Mathematics (1998)
2
For any two vectors $$u$$ and $$v,$$ prove that
(a) $${\left( {u\,.\,v} \right)^2} + {\left| {u \times v} \right|^2} = {\left| u \right|^2}{\left| v \right|^2}$$ and
(b) $$\left( {1 + {{\left| u \right|}^2}} \right)\left( {1 + {{\left| v \right|}^2}} \right) = {\left( {1 - u.v} \right)^2} + {\left| {u + v + \left( {u \times v} \right)} \right|^2}.$$
(a) $${\left( {u\,.\,v} \right)^2} + {\left| {u \times v} \right|^2} = {\left| u \right|^2}{\left| v \right|^2}$$ and
(b) $$\left( {1 + {{\left| u \right|}^2}} \right)\left( {1 + {{\left| v \right|}^2}} \right) = {\left( {1 - u.v} \right)^2} + {\left| {u + v + \left( {u \times v} \right)} \right|^2}.$$
Answer
B
C
D
3
Prove, by vector methods or otherwise, that the point of intersection of the diagonals of a trapezium lies on the line passing through the mid-points of the parallel sides. (You may assume that the trapezium is not a parallelogram.)
Answer
(B)
Vector methods can easily prove this by expressing the position vectors of the intersection point and midpoints and showing collinearity.
7
Let $${C_1}$$ and $${C_2}$$ be the graphs of the functions $$y = {x^2}$$ and $$y = 2x,$$ $$0 \le x \le 1$$ respectively. Let $${C_3}$$ be the graph of a function $$y=f(x),$$ $$0 \le x \le 1,$$ $$f(0)=0.$$ For a point $$P$$ on $${C_1},$$ let the lines through $$P,$$ parallel to the axes, meet $${C_2}$$ and $${C_3}$$ at $$Q$$ and $$R$$ respectively (see figure.) If for every position of $$P$$ (on $${C_1}$$ ), the areas of the shaded regions $$OPQ$$ and $$ORP$$ are equal, determine the function$$f(x).$$
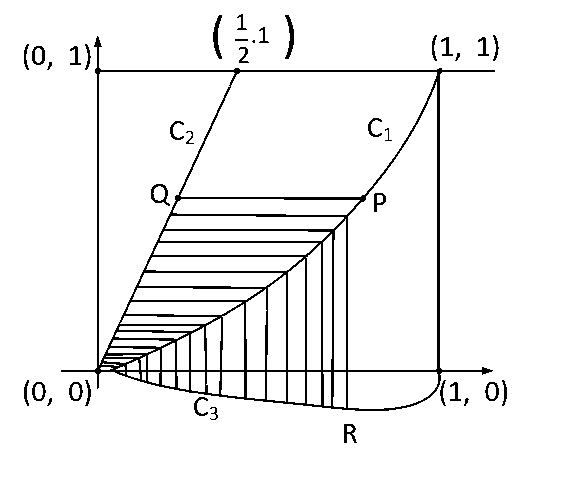

Answer
(C)
f(x) = x^3 - x^2
8
Three players, $$A,B$$ and $$C,$$ toss a coin cyclically in that order (that is $$A, B, C, A, B, C, A, B,...$$) till a head shows. Let $$p$$ be the probability that the coin shows a head. Let $$\alpha ,\,\,\,\beta $$ and $$\gamma $$ be, respectively, the probabilities that $$A, B$$ and $$C$$ gets the first head. Prove that $$\beta = \left( {1 - p} \right)\alpha $$ Determine $$\alpha ,\beta $$ and $$\gamma $$ (in terms of $$p$$).
Answer
(A)
$$\alpha = \frac{p}{1 - (1-p)^3}, \beta = \frac{(1-p)p}{1 - (1-p)^3}, \gamma = \frac{p(1-p)^2}{1 - (1-p)^3}$$
25
[Hint: You may use the fact that $${\left( {1 + x} \right)^{\left( {m + 1} \right)p}} = {\left( {1 + x} \right)^p}{\left( {1 + x} \right)^{mp}}$$]
Answer
(A)
The problem asks to prove a divisibility property of binomial coefficients involving a prime number p. The hint suggests using the binomial theorem and induction.
36
Suppose $$f(x)$$ is a function satisfying the following conditions
(a) $$f(0)=2,f(1)=1$$,
(b) $$f$$has a minimum value at $$x=5/2$$, and
(c) for all $$x$$, $$$f'\left( x \right) = \matrix{ {2ax} & {2ax - 1} & {2ax + b + 1} \cr b & {b + 1} & { - 1} \cr {2\left( {ax + b} \right)} & {2ax + 2b + 1} & {2ax + b} \cr } $$$
where $$a,b$$ are some constants. Determine the constants $$a, b$$ and the function $$f(x)$$.
(a) $$f(0)=2,f(1)=1$$,
(b) $$f$$has a minimum value at $$x=5/2$$, and
(c) for all $$x$$, $$$f'\left( x \right) = \matrix{ {2ax} & {2ax - 1} & {2ax + b + 1} \cr b & {b + 1} & { - 1} \cr {2\left( {ax + b} \right)} & {2ax + 2b + 1} & {2ax + b} \cr } $$$
where $$a,b$$ are some constants. Determine the constants $$a, b$$ and the function $$f(x)$$.
Answer
(A)
$$a = 1/4, b = -5/4, f(x) = (1/4)x^2 - (5/4)x + 2$$
42
A bird flies in a circle on a horizontal plane. An observer stands at a point on the ground. Suppose $${60^ \circ }$$ and $${30^ \circ }$$ are the maximum and the minimum angles of elevation of the bird and that they occur when the bird is at the points $$P$$ and $$Q$$ respectively on its path. Let $$\theta $$ be the angle of elevation of the bird when it is a point on the are of the circle exactly midway between $$P$$ and $$Q$$. Find the numerical value of $${\tan ^2}\theta $$. (Assume that the observer is not inside the vertical projection of the path of the bird.)
Answer
(C)
3/5
45
If$$\,\,\,$$ $$y = {{a{x^2}} \over {\left( {x - a} \right)\left( {x - b} \right)\left( {x - c} \right)}} + {{bx} \over {\left( {x - b} \right)\left( {x - c} \right)}} + {c \over {x - c}} + 1$$,
prove that $${{y'} \over y} = {1 \over x}\left( {{a \over {a - x}} + {b \over {b - x}} + {c \over {c - x}}} \right)$$.
prove that $${{y'} \over y} = {1 \over x}\left( {{a \over {a - x}} + {b \over {b - x}} + {c \over {c - x}}} \right)$$.
Answer
(D)
Take the natural logarithm of both sides and then differentiate.

