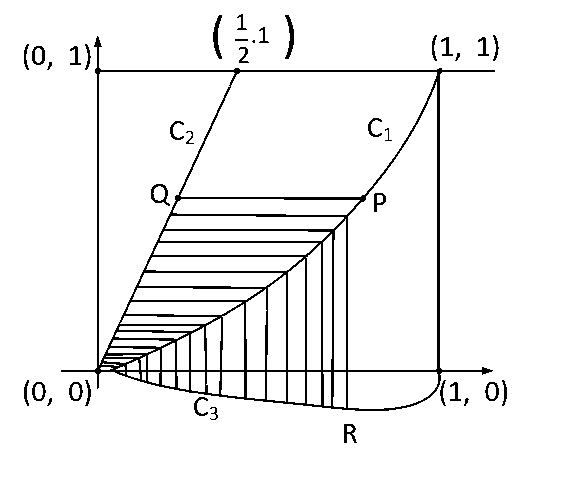
Let $${C_1}$$ and $${C_2}$$ be the graphs of the functions $$y = {x^2}$$ and $$y = 2x,$$ $$0 \le x \le 1$$ respectively. Let $${C_3}$$ be the graph of a function $$y=f(x),$$ $$0 \le x \le 1,$$ $$f(0)=0.$$ For a point $$P$$ on $${C_1},$$ let the lines through $$P,$$ parallel to the axes, meet $${C_2}$$ and $${C_3}$$ at $$Q$$ and $$R$$ respectively (see figure.) If for every position of $$P$$ (on $${C_1}$$ ), the areas of the shaded regions $$OPQ$$ and $$ORP$$ are equal, determine the function$$f(x).$$