WAEC - Physics (2020 - No. 34)
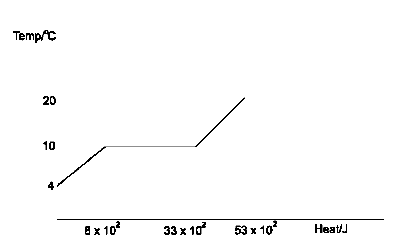
The sketched graph above illustrates the heating curve of a 0.02kg of water. Determine the approximate value of the specific latent heat of vapourization of water
Explanation
specific latent heat of vapourization is the amount of heat energy needed to change 1kg of liquid to vapour without a temperature change. The heat absorbed by the liquid at the beginning of vapourization is \(8 \times 10^3\)J and heat absorbed after the change of stage is \(53 \times 10^3\)J. therefore, the total heat energy needed to change the liquid completely to vapour is Q = \(53 \times 10^3 - 8 \times 10^3 J = 45 \times10^3\)J
Recall, Q = mL
Where, L = specific latent heat of vapourization
Q = mL
L = \(\frac{ Q}{m}\) = \(\frac{ 45 \times 10^3}{0.02}\)
L = \(2.25 \times10^6JKg^{-1}\)
Comments (0)


