WAEC - Physics (1990 - No. 44)
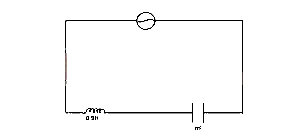
If the frequency of the ac. circuit illustrated above is 500/π Hz what would be the reactance in the circuit?
(Inductance (L) = 0.9H, Capacitance (C) = \(2 \times 10^{-6}\)
Explanation
Given Data: Frequency (F) = \(\frac{500}{π}\) , Inductance (L) = 0.9H, Capacitance (C) = \(2 \times 10^{-6}\)
Total circuit reactance = Inductive reactance ( X\(_L\) ) - Capacitive reactance ( X\(_C\) )
when ( X\(_L\) ) > ( X\(_C\) )
Inductive reactance ( X\(_L\) ) = 2πFL = 2 \(\times\) π \(\times\) \(\frac{500}{π}\) \(\times\) 0.9 = 900Ω
Capacitive reactance ( X\(_C\) ) = \(\frac{1}{2πFC}\) = \(\frac{1}{2 \times π \times 500/π \times 2 \times 10^{-6}}\)
= \(\frac{1}{2 \times 10^{-3}}\) = \(\frac{1}{0.002}\)
= 500Ω
Total circuit reactance = ( X\(_L\) ) - ( X\(_C\) ) = (900 - 500)Ω
=400Ω
Comments (0)


