WAEC - Mathematics (2024 - No. 21)
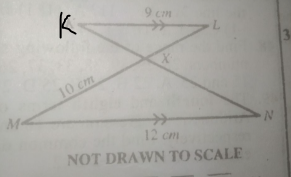
In the diagram above, \(\overline{MN} || \overline{KL}\), \(\overline{ML}\) and \(\overline{KN}\) intersect at X. |\(\overline{MN}\)| = 12cm, |\(\overline{MX}\)| = 10cm and |\(\overline{MN}\)| = 9cm. If the area of \(\triangle\) MXN is 16cm\(^2\), calculate the area of \(\triangle\) LXK
9cm\(^2\)
8cm\(^2\)
10cm\(^2\)
12cm\(^2\)
Explanation
\(\overline{MN} || \overline{KL}\), \(\triangle\) LXK is similar to \(\triangle\)MXN
So, the ratio of the areas of the two similar triangles equals the square of the ratio of their corresponding sides
Therefore, \(\frac{ Area of \triangle MXN}{Area of \triangle LXK} = \frac{12^2}{9^2}\)
\(\frac{16}{Area of \triangle LXK} = \frac{144}{81}\)
Area of \(\triangle\)LXK = \(\frac{ 16 \times 81}{144} = 9cm^2\)
Comments (0)


