WAEC - Mathematics (2023 - No. 1)
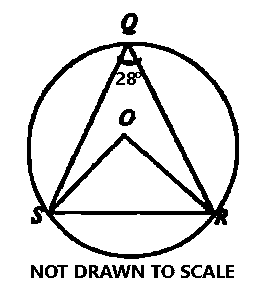
In the diagram, O is the center of the circle QRS and ∠SQR = 28°. Find ∠ORS.
\(56^0\)
\(28^0\)
\(76^0\)
\(62^0\)
Explanation
∠SOR = 2 × 28° = 56° (angle at the centre is twice the angle at the circumference)
From ∆SOR
|OS| = |OR| (radii)
So, ∆SOR is isosceles.
∠ORS = \(\frac{180^0 - 56^0}{2} = \frac{124^0}{2}\) ( base angles of isosceles triangle are equal)
∴ ∠ORS = 62°
Comments (0)


