WAEC - Mathematics (1999 - No. 21)
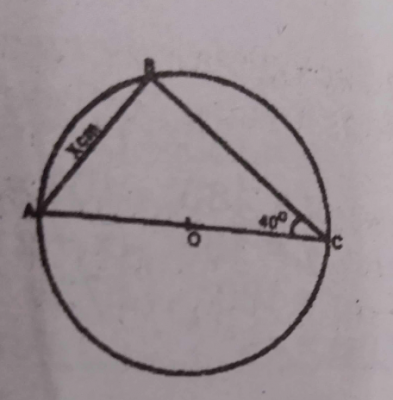
From the diagram above. ABC is a triangle inscribed in a circle center O. ∠ACB = 40º and |AB| = x cm. Calculate the radius of the circle.
\(\frac{x}{sin 40^o}\)
\(\frac{x}{cos 40^o}\)
\(\frac{x}{2 sin 40^o}\)
\(\frac{x}{2 cos 40^o}\)
Explanation
In the diagram given in the question, < ABC = 90º ( < in a semi-circle)
In triangle ABC, Sin 40º = \(\frac{x}{|AC|}\)
|AC| = \(\frac{x}{sin40º}\)
Since |AC| is a diameter, radius is half of |AC| = \(\frac{x}{2sin40º}\)
Comments (0)


