WAEC - Mathematics (1992 - No. 28)

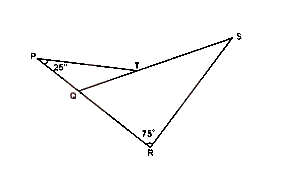
In the diagram above, PQT is an isosceles triangle.|PQ| = |QT|, ∠SRQ = 75°, ∠QPT = 25° and PQR is straight line. Find ∠RST

20^o

50^o

55^o

70^o

75^o

< PTQ = 25° (base angles of an isos. triangle)

\(\therefore\) < PQT = 180° - (25° + 25°) = 130° (sum of angles in triangle PQT)

\(\therefore\) < RST = 130° - 75° = 55° (exterior angle = sum of 2 opp. interior angles)