WAEC - Mathematics (1989 - No. 20)
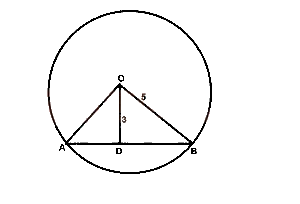
In the diagram above, O is the center of the circle. Calculate the length of the chord AB if |OA| = 5cm, |OD| = 3cm and ∠AOD = ∠BOD
3cm
4cm
5cm
8cm
15cm
Explanation
In \(\Delta DOB\), let < DOB = \(\alpha\)
In \(\Delta DOB\), \(5^2 = 3^2 + s^2\)
\(s^2 = 25 - 9 = 16\)
\(s = 4cm\)
\(\sin \alpha = \frac{4}{5}\)
\(\alpha = \frac{< AOB}{2}\)
Length of chord = \(2r \sin (\frac{\theta}{2})\)
|OB| = r = 5cm
L = \(2(5)(\frac{4}{5})\)
= 8 cm
Comments (0)


