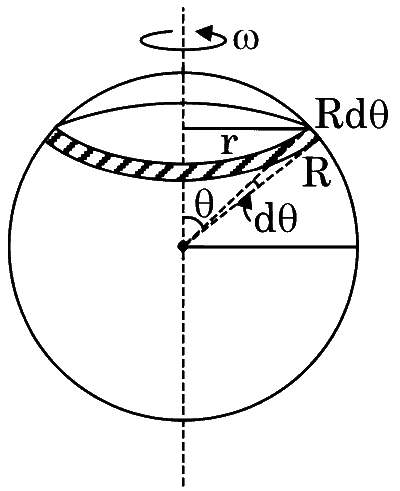
$\begin{aligned} & \mathrm{dM}=\mathrm{dIA} \\ & \mathrm{A}=\pi \mathrm{r}^2=\pi(\mathrm{R} \sin \theta)^2 \\ & \mathrm{dI}=\frac{\mathrm{da}}{\mathrm{T}}=\frac{\sigma(2 \pi \mathrm{r})(\mathrm{R} \mathrm{d} \theta) \omega}{2 \pi} \\ & \mathrm{dI}=\frac{\sigma 2 \pi \mathrm{R}^2 \omega \sin \theta \mathrm{~d} \theta}{2 \pi}\end{aligned}$

$$ \mathrm{dI}=\sigma \mathrm{R}^2 \omega \sin \theta \mathrm{~d} \theta $$

Magnetic dipole moment :

$$ \begin{aligned} & M=\int d M=\int_0^\pi \sigma R^2 \omega \pi R^2 \sin ^3 \theta d \theta \\ & M=\sigma R^4 \omega \pi \int_0^\pi \sin ^3 \theta d \theta \quad\left(\because \int_0^\pi \sin ^3 \theta d \theta=\frac{4}{3}\right) \\ & M=\left(\frac{Q}{4 \pi R^2}\right) R^4 \omega \pi\left(\frac{4}{3}\right) \end{aligned} $$

Magnetic dipole moment

$$ \mathrm{M}=\frac{\mathrm{QR}^2 \omega}{3} $$

Angular momentum

$$ \begin{aligned} & \mathrm{L}=\left(\frac{2}{5} \mathrm{MR}^2\right) \omega \\ & \frac{\mathrm{M}}{\mathrm{~L}}=\frac{\mathrm{QR}^2 \omega}{3 \times \frac{2}{5} \mathrm{MR}^2 \omega}=\frac{\mathrm{Q}}{2 \mathrm{M}}\left(\frac{5}{3}\right) \end{aligned} $$

$\alpha=\frac{5}{3}=1.67$